The idea of the curl of a vector field
The divergence and curl of a vector field are two vector operators whose basic properties can be understood geometrically by viewing a vector field as the flow of a fluid or gas. Divergence is discussed on a companion page. Here we give an overview of basic properties of curl than can be intuited from fluid flow.
The curl of a vector field captures the idea of how a fluid may rotate. Imagine that the below vector field $\dlvf$ represents fluid flow. The vector field indicates that the fluid is circulating around a central axis.

Applet loading
A rotating vector field. If the vector field is interpreted as velocity of fluid flow, the fluid appears to flow in circles. From the graph's original perspective (i.e., before you rotate it with the mouse), the fluid appears to circulate in a counter clockwise fashion. If you rotate the graph, you might see dots floating along the axis of rotation. These dots are representations of vectors of zero length, as the velocity is zero there.
This macroscopic circulation of fluid around circles (i.e., the rotation you can easily view in the above graph) actually is not what curl measures. But, it turns out that this vector field also has curl, which we might think of as “microscopic circulation.” To test for curl, imagine that you immerse a small sphere into the fluid flow, and you fix the center of the sphere at some point so that the sphere cannot follow the fluid around. Although you fix the center of the sphere, you allow the sphere to rotate in any direction around its center point. The rotation of such a sphere is illustrated in the below applet. The rotation of the sphere measures the curl of the vector field $\dlvf$ at the point in the center of the sphere. (The sphere should actually be really really small, because, remember, the curl is microscopic circulation.)
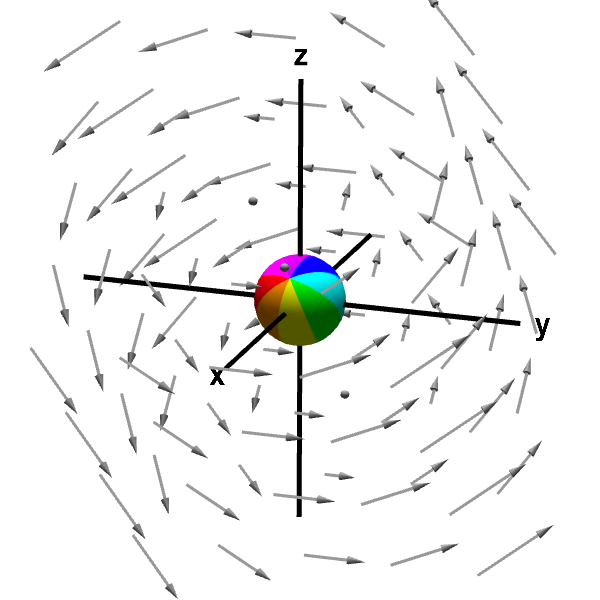
Applet loading
A sphere rotated by a rotating vector field. A sphere is embedded in a rotating fluid whose velocity is given by the vector field. The middle of the sphere is anchored to a point (originally, the origin), but it is allowed to rotate with the fluid. The rotation of the sphere by the fluid is an indication of the curl of the vector field. You can move the point at which the sphere is anchored by dragging it with your mouse.
The vector field $\dlvf$ determines both in what direction the sphere rotates, and the speed at which it rotates. We define the curl of $\dlvf$, denoted $\curl \dlvf$, by a vector that points along the axis of the rotation and whose length corresponds to the speed of the rotation. (As the curl is a vector, it is very different from the divergence, which is a scalar.)
We can draw the vector corresponding to $\curl \dlvf$ as follows. We make the length of the vector $\curl \dlvf$ proportional to the speed of the sphere's rotation. The direction of $\curl \dlvf$ points along the axis of rotation, but we need to specify in which direction along this axis the vector should point. We will (arbitrarily?) set the direction of the curl vector by using the following “right hand rule.” To see where $\curl \dlvf$ should point, curl the fingers of your right hand in the direction the sphere is rotating; your thumb will point in the direction of $\curl \dlvf$. For our example, $\curl \dlvf$ is shown by the green arrow.
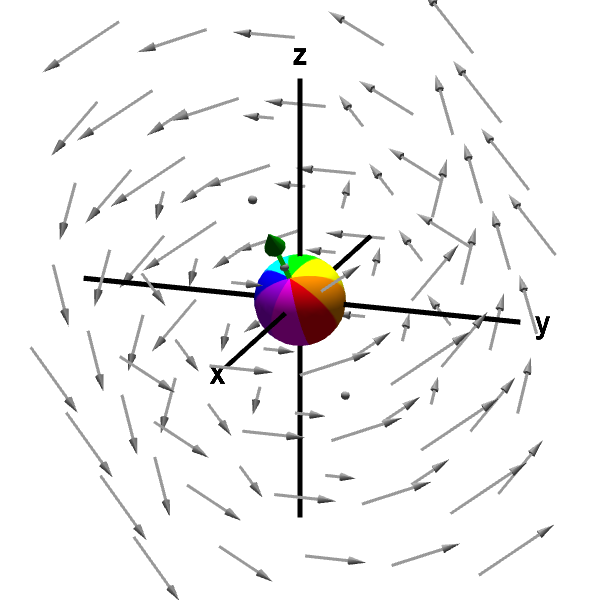
Applet loading
A rotating sphere indicating the presence of curl. The green arrow along the sphere's axis of rotation is the curl of the vector field. You can rotate the graph to see the green arrow better. The length of the arrow corresponds to the speed of rotation, and the direction of the arrow is determined by the right hand rule. You can move the point at which the sphere is anchored by dragging it with your mouse. For this example, the curl is constant throughout the vector field, so the green arrow and the sphere's spinning remains unchanged as you move the sphere around.
For this particular vector field, it turns out that $\curl \dlvf$ doesn't change with position (this, of course, is not true in general). For example, if we move the sphere to another location, it will still spin in the same direction with the same speed. Notice how the sphere spins the same way if you move the sphere to a different location in the above applets. (See the applet's page for more information.)
The curl is a three-dimensional vector, and each of its three components turns out to be a combination of derivatives of the vector field $\dlvf$. You can read about one can use the same spinning spheres to obtain insight into the components of the vector $\curl \dlvf$. The formula for the curl components may seem ugly at first, and some clever notation can help you remember the formula. Once you have the formula, calculating the curl of a vector field is a simple matter, as shown by this example.
Thread navigation
Multivariable calculus
- Previous: Subtleties about divergence
- Next: Subtleties about curl
Math 2374
Similar pages
- Subtleties about curl
- The components of the curl
- Divergence and curl notation
- Divergence and curl example
- The idea behind Green's theorem
- The definition of curl from line integrals
- Calculating the formula for circulation per unit area
- A path-dependent vector field with zero curl
- The idea behind Stokes' theorem
- The idea of the divergence of a vector field
- More similar pages