The components of the curl
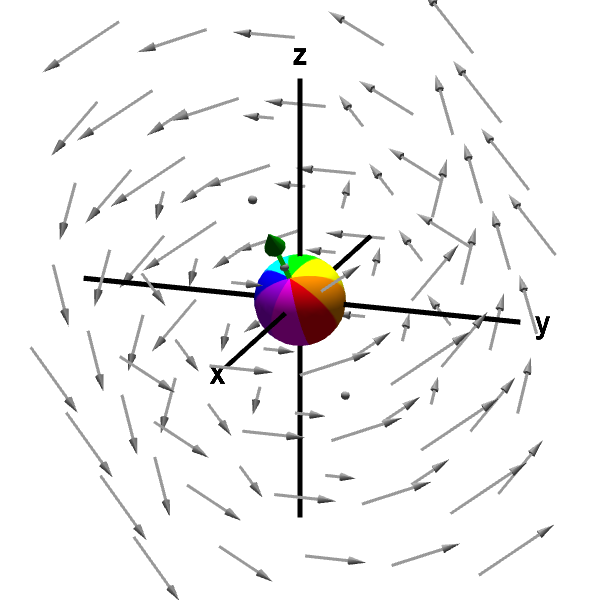
Recall that one can visualize the curl of a three-dimensional vector field $\dlvf=(\dlvfc_1,\dlvfc_2,\dlvfc_3)$ by inserting a small sphere into a fluid with flow given by $\dlvf$, fixing the center of the sphere, and allowing the sphere to rotate in any direction. The direction of the vector $\curl \dlvf$ is given using the right hand rule, and the magnitude $\| \curl \dlvf \|$ is given by the speed at which the sphere rotates, as shown in the following figure.
Applet loading
A rotating sphere indicating the presence of curl. The green arrow along the sphere's axis of rotation is the curl of the vector field. You can rotate the graph to see the green arrow better. The length of the arrow corresponds to the speed of rotation, and the direction of the arrow is determined by the right hand rule. You can move the point at which the sphere is anchored by dragging it with your mouse. For this example, the curl is constant throughout the vector field, so the green arrow and the sphere's spinning remains unchanged as you move the sphere around.
Since $\curl \dlvf$ is a three-dimensional vector, it has components in the $x$, $y$, and $z$ directions. If we let $\vc{v} = \curl \dlvf$, then we could write $\curl \dlvf$ in terms of components as $$\curl \dlvf = \vc{v} = v_1 \vc{i} + v_2 \vc{j} + v_3 \vc{k}.$$ To visualize the components of the curl, we can use the rotating sphere animation with just small modifications.
$z$-component of curl
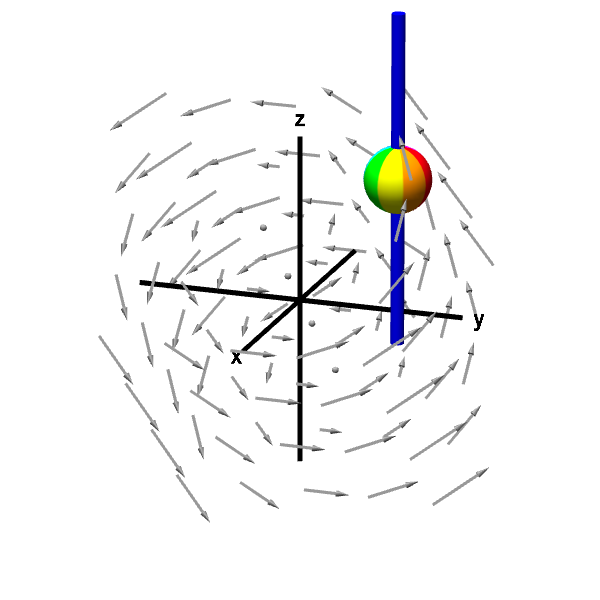
To visualize $v_3$, the component of the curl in the $z$ direction, we could place our sphere in the fluid as before, only with one important difference. Rather than allowing the sphere to rotate in any direction, we place the sphere on a rod that is parallel to the $z$-axis. The rod allows the sphere to rotate only around the axis of the rod. Using the right hand rule, we see that the “direction vector” corresponding to the rotation must point along the rod, i.e., it is parallel to the $z$-axis. In fact, this rotation corresponds $v_3 \vc{k}$, where $v_3$ is the component of the curl in the $z$ direction. The speed of the rotation corresponds to $|v_3|$, while the sign of $v_3$ indicates the direction of rotation around the axis.
Applet loading
A rotating sphere on a rod gives z-component of curl. The rod constrains the rotation of the sphere to point (using the right hand rule) in either the positive or negative $z$ direction. The speed of this rotation corresponds to the $z$-component of the curl.
From the above animation, we see that that the sphere is rotating in a counterclockwise direction when viewed from the positive $z$-axis. This rotation means that the component of the curl in the $z$ direction is positive (using the right hand rule). If the sphere were rotating clockwise when viewed from the positive $z$-axis, then the component of the curl in the $z$ direction would be negative. Since $\curl \dlvf$ is not parallel to the $z$-axis, the magnitude of the $z$-component $v_3$ is smaller than the magnitude of $\curl \dlvf$, and the sphere is rotating more slowly than it did when it was allowed to rotate freely.
You can visualize that there is also “macroscopic circulation” in this same direction by rotating the figure so that the $z$-axis is coming straight out of the screen. Viewed from that axis, the vector field still appears to circulate. (Remember, of course, that this “macroscopic circulation” doesn't neccesarily correspond to the “microscopic circulation” of the curl.)
Notice that when the sphere is fixed to the rod, it cannot response to the $z$-component of the vector field; any push up or down of the fluid cannot affect the movement of the sphere. We can immediately deduce that the $z$-component of the curl should not depend on the $z$-component of $\dlvf$.
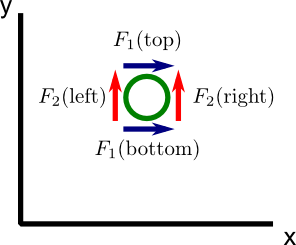
What properties of the vector field $\dlvf$ will cause the sphere to spin even when it is fixed to the rod? Since we can ignore the $z$-component $\dlvfc_3$, we know the spinning must depend only on the $x$-component $\dlvfc_1$ or the $y$-component $\dlvfc_2$ of the vector field. Let's look at a slice of the vector field through the sphere that is parallel to the $xy$-plane, as illustrated below. This image is intended to represent the view of the above applet when rotated so that the $z$-axis is coming out of the screen. However, to make the visualization easier, we moved the sphere (illustrated as a circle) to the right so that it isn't on top of the $y$-axis.
A positive $z$-component $v_3$ of the curl corresponds to counterclockwise rotation from this view. One way to induce a counterclockwise rotation, would be to have the upward push of the vector field on the right of the sphere be greater than the upward push on the left of the sphere. This upward push corresponds to the the $y$-component $\dlvfc_2$ (illustrated by red arrows) of the vector field. The curl is supposed to correspond to “microscopic circulation,” so we view the sphere is being very small. The increase of $\dlvfc_2$ as we move a tiny bit to the right (i.e., increase $x$) is captured by the partial derivative of $\dlvfc_2$ with respect to $x$. Hence, it seems reasonable that a positive $\pdiff{\dlvfc_2}{x}$ would tend to lead to counterclockwise rotation from the point of view of our picture, which is a rotation corresponding to a positive $z$-component of the curl. A negative $\pdiff{\dlvfc_2}{x}$ would tend to induce clockwise rotation, or a negative $z$-component of the curl.
We could also induce counterclockwise rotation by having the righward push of the vector field be larger on the bottom of the sphere than on the top. Since this corresponds to $\dlvfc_1$ (illustrated by blue arrows) decreasing as $y$ increases, we need a negative $\pdiff{\dlvfc_1}{y}$ to increase counterclockwise rotation and make the $z$-component of the curl be larger.
We conclude that particular changes (i.e., derivatives) of $\dlvfc_1$ and $\dlvfc_2$ lead to the sphere spinning in a direction corresponding to the $z$-component of the curl. It turns out that the effects of these changes in $\dlvf$ simply add up. Although we need line integrals in order to fill in all the details, the above picture at least gives some intuition why the $z$-component of the the curl is $$v_3 = \curl \dlvf \cdot \vc{k} = \pdiff{\dlvfc_2}{x} - \pdiff{\dlvfc_1}{y}.$$
In the above discussion, we were able to ignore the $z$-component of the vector field as well as any dependence of the vector field on $z$. Nothing would have changed if we had been discussing a two-dimensional vector field in $\vc{x}$ and $\vc{y}$. Hence the quantity $\pdiff{\dlvfc_2}{x} - \pdiff{\dlvfc_1}{y}$ also corresponds to the counterclockwise “microscopic circulation,” of a vector field in the plane, which shows up, for example, in Green's theorem.
$y$-component of curl
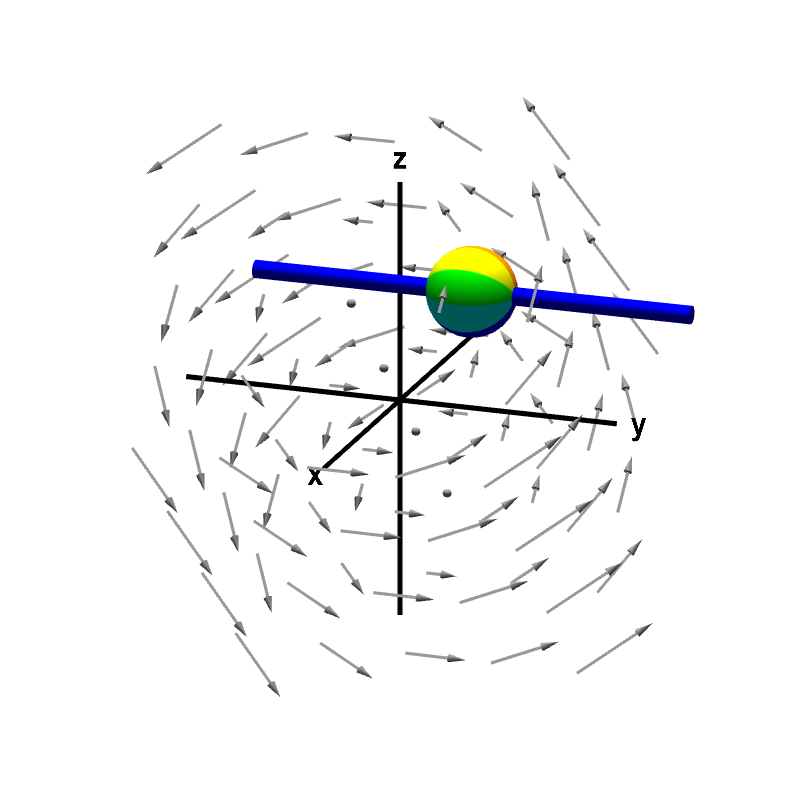
Glancing at the original animation where the sphere can rotate in any direction, we can see that the green arrow corresponding to the curl is perpendicular to the $y$-axis. For our particular example vector field, we can see the component $\curl \dlvf$ in the $y$ direction is zero. If we placed the sphere on a rod that is parallel to $y$ axis, the fluid flow would not make the sphere rotate.
Applet loading
A nonrotating sphere on a rod shows no y-component of curl. The rod constrains the rotation of the sphere to point (using the right hand rule) in either the positive or negative $y$ direction. The speed of this rotation corresponds to the $y$-component of the curl. In this case, the sphere does not rotate, indicating the $y$-component of the curl is zero.
If you rotate the above figure so that the $y$-axis is coming straight out of the screen, you can see that the vector field no longer looks like it is rotating. (Though, remember, this isn't a true test of curl, which is “microscopic circulation.”) We can still calculate the component of $\curl \dlvf$ parallel to the $y$-axis. If we used the same calculation as we did the for $z$-component, we would conclude that the $y$-component of the curl is $$v_2 = \curl \dlvf \cdot \vc{j} = \pdiff{\dlvfc_1}{z} - \pdiff{\dlvfc_3}{x}.$$ In our example, $v_2$ is zero.
$x$-component of curl
Lastly, we can visualize the component of $\curl \dlvf$ parallel to the $x$-axis by placing the sphere on a rod parallel to the $x$-axis. Looking at the green arrow in the first animation, we see this should be nonzero for our example, and the below animation verifies this. As above, we could calculate this component of the curl as $$v_1 = \curl \dlvf \cdot \vc{i} = \pdiff{\dlvfc_3}{y}-\pdiff{\dlvfc_2}{z}.$$

Applet loading
A rotating sphere on a rod gives x-component of curl. The rod constrains the rotation of the sphere to point (using the right hand rule) in either the positive or negative $x$ direction. The speed of this rotation corresponds to the $x$-component of the curl.
In summary, we can see that the $\curl \dlvf$ is a vector whose components indicate the “microscopic circulation” in the $x$, $y$, and $z$ directions, respectively: $$\curl \dlvf = \biggl(\pdiff{\dlvfc_3}{y}-\pdiff{\dlvfc_2}{z}, \pdiff{\dlvfc_1}{z} - \pdiff{\dlvfc_3}{x}, \pdiff{\dlvfc_2}{x} - \pdiff{\dlvfc_1}{y} \biggr).$$
Thread navigation
Multivariable calculus
- Previous: Subtleties about curl
- Next: Divergence and curl notation
Math 2374
Similar pages
- The idea of the curl of a vector field
- Subtleties about curl
- Divergence and curl notation
- Divergence and curl example
- The idea behind Green's theorem
- The definition of curl from line integrals
- Calculating the formula for circulation per unit area
- A path-dependent vector field with zero curl
- The idea behind Stokes' theorem
- The idea of the divergence of a vector field
- More similar pages