Applet: A parametrized helicoid with surface area elements
Applet loading
Applet loading
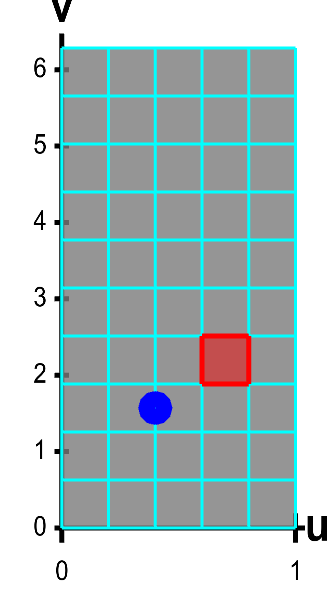
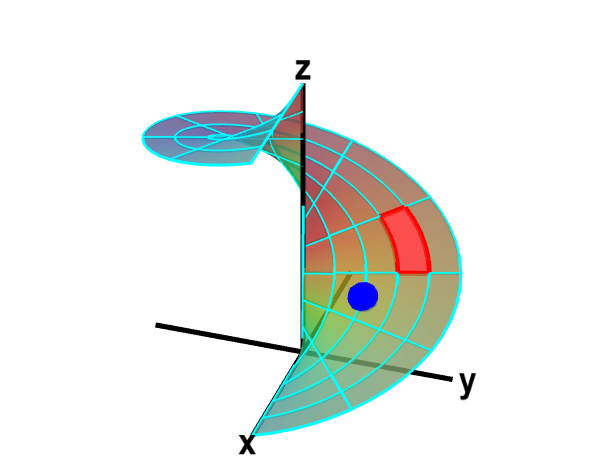
The function $\dlsp(\spfv,\spsv) = (\spfv\cos \spsv, \spfv\sin \spsv, \spsv)$ parametrizes a helicoid when $(\spfv,\spsv) \in \dlr$, where $\dlr$ is the rectangle $[0,1] \times [0, 2\pi]$. The region $\dlr$, shown as the rectangle on the left, is divided into small rectangles, which are mapped onto “curvy rectangles” on the surface at the right. To visualize the mapping, you can click on a rectangle in either panel to highlight it in red; the corresponding rectangle in the opposite panel is also hightlighted in red. The area of the red region on the helicoid depends on how $\dlsp$ stretches or shrinks the small red rectangle of $\dlr$ as it maps it on the surface. You can also drag the blue point in either $\dlr$ or the helicoid surface, and the blue point in the opposite panel moves so that the location of the right point is $\dlsp(\spfv,\spsv)$ when the location of the left point is $(\spfv,\spsv)$.
Applet links
This applet is found in the pages
- Surface area of parametrized surfaces
- Calculation of the surface area of a parametrized surface
- Introduction to a surface integral of a scalar-valued function
Notation systems
More information on notation systems
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.