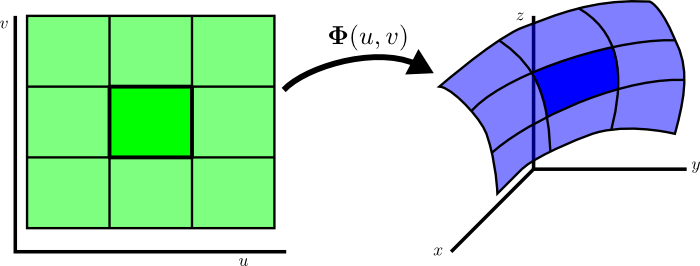
Calculation of the surface area of a parametrized surface
A parametrized surface is a mapping by a function $\dlsp: \R^2 \to \R^3$ (confused?) of a planar region $\dlr$ onto a surface floating in three dimensions. To calculate the area of this surface, we chop up the region $\dlr$ into small rectangles, as displayed below for the function \begin{align*} \dlsp(\spfv,\spsv) = (\spfv\cos \spsv, \spfv\sin \spsv, \spsv). \end{align*}.
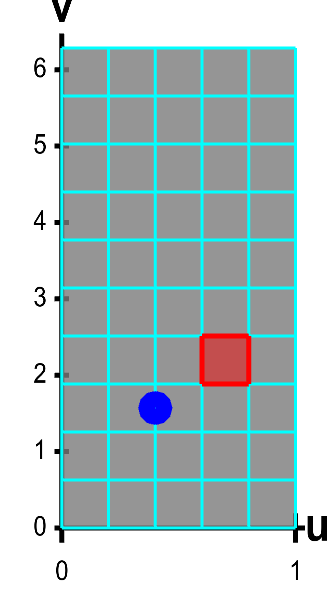
Applet loading
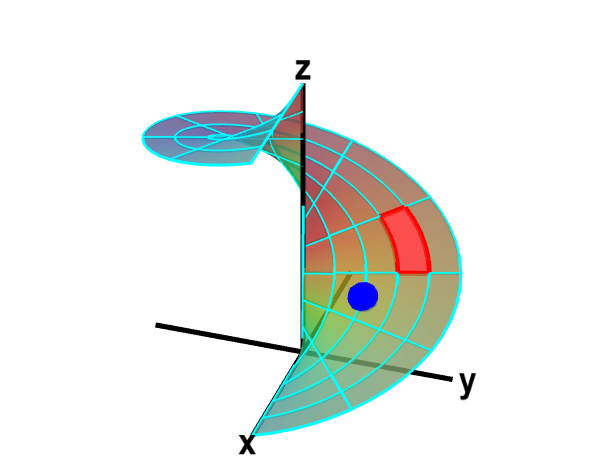
Applet loading
A parametrized helicoid with surface area elements. The function $\dlsp(\spfv,\spsv) = (\spfv\cos \spsv, \spfv\sin \spsv, \spsv)$ parametrizes a helicoid when $(\spfv,\spsv) \in \dlr$, where $\dlr$ is the rectangle $[0,1] \times [0, 2\pi]$. The region $\dlr$, shown as the rectangle on the left, is divided into small rectangles, which are mapped onto “curvy rectangles” on the surface at the right. To visualize the mapping, you can click on a rectangle in either panel to highlight it in red; the corresponding rectangle in the opposite panel is also hightlighted in red. The area of the red region on the helicoid depends on how $\dlsp$ stretches or shrinks the small red rectangle of $\dlr$ as it maps it on the surface. You can also drag the blue point in either $\dlr$ or the helicoid surface, and the blue point in the opposite panel moves so that the location of the right point is $\dlsp(\spfv,\spsv)$ when the location of the left point is $(\spfv,\spsv)$.
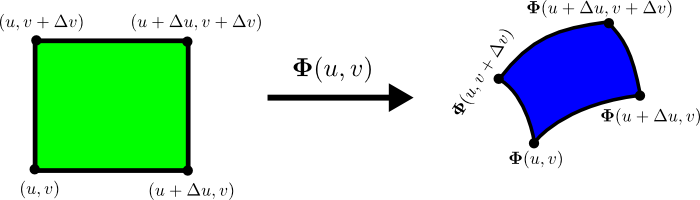
The function $\dlsp$ maps each small rectangle to a “curvy rectangle” on the surface. Here's another view of this mapping, where you have to imagine that the blue surface on the right is floating in space.
Let $\Delta \spfv$ and $\Delta \spsv$ be width and height of the small rectangle. If the lower-left corner of the rectangle is at position $(\spfv,\spsv)$, then $\dlsp$ maps the lower-left corner to the point $\dlsp(\spfv,\spsv)$ on the “curvy rectangle.”
The lower-right corner of the rectangle is the point $(\spfv+\Delta \spfv,\spsv)$, so it gets mapped to $\dlsp(\spfv+\Delta \spfv,\spsv)$. Similarly, the upper-left corner of the rectangle is mapped to $\dlsp(\spfv,\spsv + \Delta \spsv)$.
To calculate the area of the “curvy rectangle”, i.e., the image of the small rectangle under $\dlsp$, we approximate it as a parallelogram. This approximation is okay when $\Delta \spfv$ and $\Delta \spsv$ small.
One side of the parallalogram is \begin{align*} \dlsp(\spfv+\Delta \spfv,\spsv)-\dlsp(\spfv,\spsv) &= \frac{\dlsp(\spfv+\Delta \spfv,\spsv)-\dlsp(\spfv,\spsv)}{\Delta \spfv} \Delta \spfv\\ &\approx\pdiff{\dlsp}{\spfv}(\spfv,\spsv)\Delta \spfv \end{align*} when $\Delta \spfv$ is small. Similarly, when $\Delta \spsv$ is small, the other side of the parallelogram is approximatly \begin{align*} \dlsp(\spfv,\spsv+\Delta \spsv) - \dlsp(\spfv,\spsv) \approx \pdiff{\dlsp}{\spsv}(\spfv,\spsv)\Delta \spsv. \end{align*}
The area of a parallegram spanned by these vectors is the magnitude of their cross product. The area of the “curvy rectangle” is approximately \begin{align*} \Delta A=\left\|\pdiff{\dlsp}{\spfv}(\spfv,\spsv) \times \pdiff{\dlsp}{\spsv}(\spfv,\spsv)\right\| \Delta \spfv \Delta \spsv. \end{align*}
The area of the whole surface is a Riemann sum over all the small rectangles. Each term is of the above form. If we take the limits $\Delta \spfv, \Delta \spsv \to 0$, then the Riemann sum converges to a double integral, and we find that the total surface area is \begin{align*} A =\left.\iint_\dlr \left\| \pdiff{\dlsp}{\spfv}(\spfv,\spsv) \times \pdiff{\dlsp}{\spsv}(\spfv,\spsv) \right\|\right. d\spfv\,d\spsv \end{align*} as promised.
Thread navigation
Multivariable calculus
Math 2374
Notation systems
Similar pages
- Surface area of parametrized surfaces
- Parametrized surface area example
- An introduction to parametrized surfaces
- Parametrized surface examples
- Normal vector of parametrized surfaces
- Orienting surfaces
- A Möbius strip is not orientable
- Parametrization of a line
- Parametrization of a line examples
- An introduction to parametrized curves
- More similar pages