Double integral examples
To illustrate computing double integrals as iterated integrals, we start with the simplest example of a double integral over a rectangle and then move on to an integral over a triangle.
Example 1
Compute the integral \begin{align*} \iint_\dlr x y^2 dA \end{align*} where $\dlr$ is the rectangle defined by $0 \le x \le 2$ and $0 \le y \le 1$ pictured below.
Solution: We will compute the double integral as the iterated integral \begin{align*} \int_0^1 \left( \int_0^2 xy^2 dx\right) dy. \end{align*} We first integrate with respect to $x$ inside the parentheses. Similar to the procedure with partial derivatives, we must treat $y$ as a constant during this integration step. Since for any constant $c$, the integral of $cx$ is $cx^2/2$, we calculate \begin{align*} \int_0^1 \left( \int_0^2 xy^2 dx\right) dy &= \int_0^1 \left(\left. \frac{x^2}{2} y^2 \right|_{x=0}^{x=2} \right)dy\\ &= \int_0^1 \left( \frac{2^2}{2} y^2 - \frac{0^2}{2} y^2 \right)dy \\ &= \int_0^1 2 y^2 dy. \end{align*} Note that in the first line above, we wrote the limits as $x=2$ and $x=0$ so it is unambiguous that $x$ is the variable we just integrated.
To finish, we need to compute the integral with respect to $y$, which is simple. Since $x$ is gone, it's just a regular one-variable integral. We calculate that our double integral is \begin{align*} \iint_\dlr x y^2 dA &= \int_0^1 2 y^2 dy\\ &= \left. \frac{2y^3}{3} \right|_0^1 \goodbreak = \frac{2(1^3)}{3}- \frac{2(0^3)}{3} \goodbreak =\frac{2}{3}. \end{align*}
To double check our answer, we can compute the integral in the other direction, integrating first with respect to $y$ and then with respect to $x$. The only trick is to remember that when integrating with respect to $y$, we must think of $x$ as a constant. Since for any constant $c$, the integral of $cy^2$ is $cy^3/3$, we calculate \begin{align*} \iint_\dlr x y^2 dA &= \int_0^2 \left( \int_0^1 xy^2 dy\right) dx\\ &= \int_0^2 \left(\left. x \frac{y^3}{3} \right|_{y=0}^{y=1}\right)dx\\ &= \int_0^2 \frac{x}{3} dx\\ &= \left.\left.\frac{x^2}{6} \right|_0^2\right. = \frac{4}{6} = \frac{2}{3}. \end{align*} As it must, this iterated integral gives the same answer.
Example 2
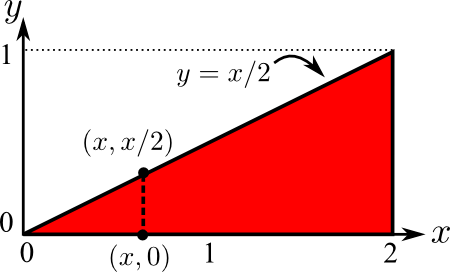
Rectangular regions are easy because the limits ($a \le x \le b$ and $c \le y \le d$) are fixed, meaning the ranges of $x$ and $y$ don't depend on each other. For regions of other shapes, the range of one variable will depend on the other. Here's an example where we integrate over the region defined by $0 \le x \le 2$ and $0 \le y \le x/2$. The fact that the range of $y$ depends on $x$ means this region is not a rectangle. In fact, the region is the triangle pictured below.
Using the same function $f(x,y)=xy^2$ as in example 1, compute $\iint_\dlr f\,dA$ where $\dlr$ is the above triangle.
Solution: A triangle is slightly more complicated than a rectangle because the limits of one variable will depend on the other variable. For the triangle defined by $0 \le x \le 2$ and $0 \le y \le x/2$, the limits of $y$ depend on $x$. For a given value of $x$, $y$ ranges from 0 to $x/2$, as illustrated above by the vertical dashed line from $(x,0)$ to $(x,x/2)$.
In a double integral, the outer limits must be constant, but the inner limits can depend on the outer variable. This means, we must put $y$ as the inner integration variables, as was done in the second way of computing Example 1. The only difference from Example 1 is that the upper limit of $y$ is $x/2$. The double integral is \begin{align*} \iint_\dlr x y^2 dA &= \int_0^2 \left(\int_0^{x/2} xy^2 dy \right) dx\\ &=\int_0^2 \left(\left.\frac{x}{3} y^3 \right|_{y=0}^{y=x/2}\right) dx\\ &=\int_0^2 \left( \frac{x}{3} \left(\frac{x}{2}\right)^3 -\frac{x}{3} 0^3 \right) dx\\ &= \int_0^2 \frac{x^4}{24} dx\\ &= \left.\left.\frac{x^5}{5\cdot 24}\right|_0^2\right. = \frac{32}{5 \cdot 24} = \frac{4}{15}. \end{align*}
Example 2'
Now compute the integral over the same triangle $\dlr$, but make $y$ be the outer integration variable.
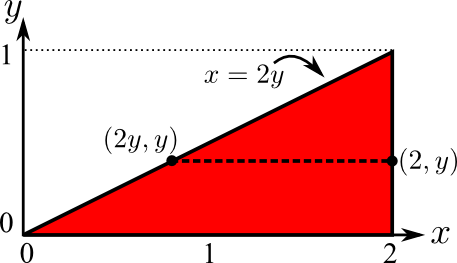
Solution: Now we need to give constant limits for $y$. As illustrated below, the total range of $y$ within the triangle is between between $0$ and $1$. Then, for a given value of $y$, $x$ takes on values between $2y$ and $2$ (as shown by the horizontal dashed line between $(2y,y)$ and $(2,y)$). Hence, we can describe the triangle by $0 \le y \le 1$ and $2y \le x \le 2$.
Is it confusing that the limits of $x$ are $2y \le x \le 2$ rather than $0 \le x \le 2$ (which would more closely parallel the above Example 2)? If we let $x$ range from $0$ to $2y$, then the triangle would be the upper-left triangle in the above picture. We want to compute the integral over the region $\dlr$, which is the lower-right triangle shaded in red. In this triangle, $y \lt x/2$ (as used above in Example 2) which means that for this example, we must use $x > 2y$.
The double integral is similar to the first way of computing Example 1, with the only difference being that the lower limit of $x$ is $2y$. The integral is \begin{align*} \iint_\dlr x y^2 dA &= \int_0^1 \left( \int_{2y}^2 xy^2 dx \right)dy\\ &= \int_0^1\left(\left.\frac{x^2y^2}{2} \right|_{x=2y}^{x=2}\right) dy\\ &= \int_0^1 \left( 2y^2 - \frac{(2y)^2 y^2}{2}\right) dy\\ &= \int_0^1 \left( 2y^2 - 2y^4\right) dy\\ &= 2 \left[ \frac{y^3}{3} - \frac{y^5}{5} \right]_0^1\\ &= 2 \left(\frac{1}{3} - \frac{1}{5} -(0-0)\right)\\ &= 2 \cdot \frac{2}{15} \goodbreak = \frac{4}{15}. \end{align*} Thankfully, this does agree with the answer we obtained in Example 2.
More examples
To go from Example 2 to Example 2', we “changed the order of integration.” You can see more examples of changing the order of integration in double integrals. You can also see more double integral examples from the special cases of interpreting double integrals as area and double integrals as volume.
Thread navigation
Multivariable calculus
- Previous: Double integrals as iterated integrals
- Next: Double integrals as volume
Math 2374
- Previous: Double integrals as iterated integrals
- Next: Double integrals as volume
Similar pages
- Introduction to double integrals
- Double integrals as iterated integrals
- Double integrals as volume
- Examples of changing the order of integration in double integrals
- Double integrals as area
- Double integrals where one integration order is easier
- Introduction to changing variables in double integrals
- Area calculation for changing variables in double integrals
- Double integral change of variable examples
- The integrals of multivariable calculus
- More similar pages