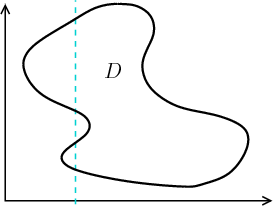Double integrals where one integration order is easier
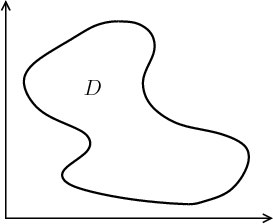
Suppose you need to calculate the double integral $\iint_\dlr f(x,y)\,dA$ for some function $f(x,y)$ and the region $\dlr$ shown below.
To calculate the double integral, you can write it as an iterated integral. For example, let's say that in the region $\dlr$, the lowest value of $y$ is $a$ and the highest value of $y$ is $b$. In other words, the range of $y$ in the region $\dlr$ is $a \le y \le b$.
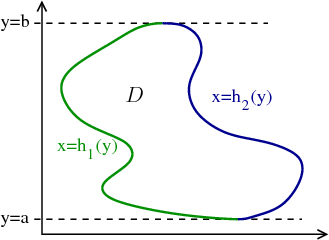
For a given value of $y$, the range of $x$ in $\dlr$ depends on the value of $y$. However, the region is nice enough so that the range of $x$ for any $y$ is just a simple interval. We could define two functions $h_1(y)$ and to $h_2(y)$ so that this interval in $x$ is $[h_1(y),h_2(y)]$ for each value of $y$. This description of the region $\dlr$ is shown in the following picture.
Since the region $\dlr$ is defined by \begin{gather*} a \le y \le b,\\ h_1(y) \le x \le h_2(y), \end{gather*} we can represent double integral of $f(x,y)$ over $\dlr$ as the following iterated integral, \begin{align*} \iint_\dlr f(x,y) dA = \int_a^b \left( \int_{h_1(y)}^{h_2(y)} f(x,y) dx \right) dy. \end{align*}
However, we would run into trouble if we tried to change the order of integration so that we integrated with respect to $y$ first. The difficulty is that the range of $y$ for some values of $x$ is not a simple interval. For example, for the value of $x$ given by the vertical dashed line below, the range of $y$ is two different intervals.
Since we cannot always write the range of $y$ as a single interval $[g_1(x),g_2(x)]$, we cannot write the integral $\iint_\dlr f(x,y)\,dA$ as a single iterated integral of the form \begin{align*} \iint_\dlr f(x,y) dA = \int_c^d \left( \int_{g_1(x)}^{g_2(x)} f(x,y) dy \right) dx. \end{align*} If we really wanted to integrate with respect to $y$ first, we'd have to break the region $\dlr$ into pieces and compute separate integrals for each piece. We'll leave that procedure to your imagination.
Thread navigation
Multivariable calculus
- Previous: Examples of changing the order of integration in double integrals
- Next: Introduction to triple integrals
Math 2374
Similar pages
- Examples of changing the order of integration in double integrals
- Introduction to double integrals
- Double integrals as iterated integrals
- Double integral examples
- Double integrals as volume
- Double integrals as area
- Triple integral examples
- Introduction to changing variables in double integrals
- Area calculation for changing variables in double integrals
- Double integral change of variable examples
- More similar pages