Forming planes
In this page, we outline ways to specify a plane.
Plane determined by point and normal vector
Given a point $P$, there are many planes that contain $P$. However, assuming that we are living in three-dimensional space ($\R^3$), a plane is uniquely determined if we also specify a normal vector $\vc{n}$ (i.e., a vector that is perpendicular to the plane).
The following applet illustrates this fact. You can experiment with changing the point $P$ and the normal vector $\vc{n}$ and see how the plane changes.
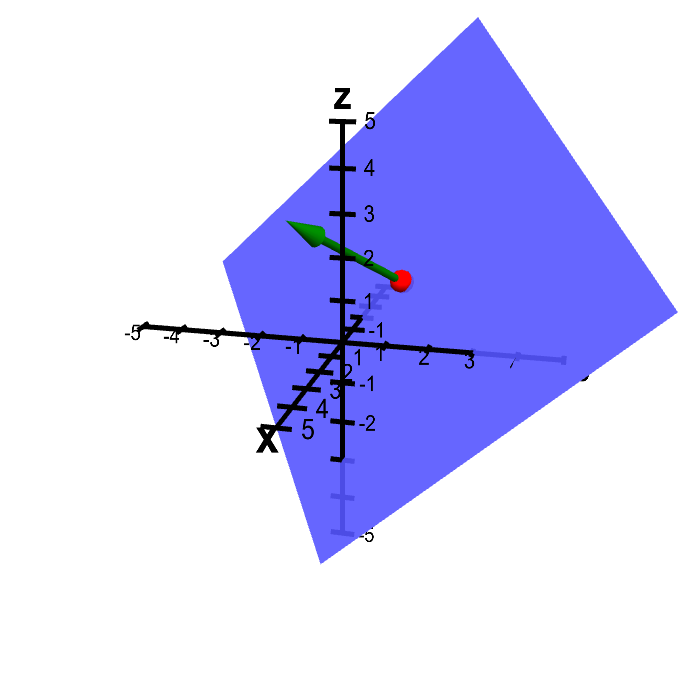
Applet loading
Plane from point and normal vector. You can change the point $\color{red}{P}$ (in red) and the normal vector $\color{green}{\vc{n}}$ (in green) by dragging the colored balls. Dragging the mouse elsewhere rotates the whole figure.
Note that the plane doesn't care about the length of $\vc{n}$, only its direction. In fact, if you change $\vc{n}$ to point in the opposite direction, you still get the same plane back. Of course, changing $P$ to any other point on the plane, wouldn't change the plane either. (The plane should really extend out to infinity in all directions, so sliding it from side to side wouldn't actually change the plane.)
We can infer the equation for the plane from these properties. Let $\vc{a}$ be the vector representing the point $P$ (i.e., the vector from the origin to $P$). Let $\vc{x}=(x,y,z)$ be the vector representing another point $Q$ on the plane. Since we know $Q$ is in the plane, can you think of any condition on the vector from $P$ to $Q$, i.e., the vector $\vc{x} - \vc{a}$? In below applet, see if you can infer the relationship between the vector $\vc{x} - \vc{a}$ and the vector $\vc{n}$.
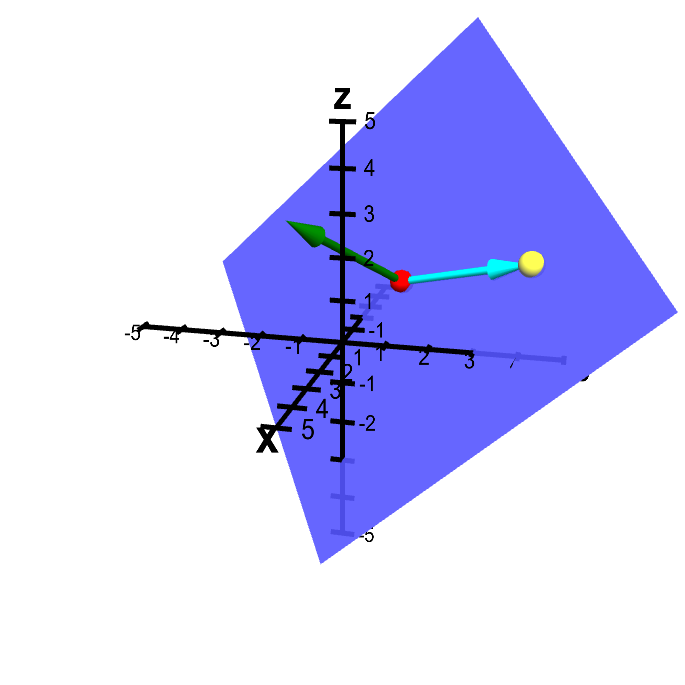
Applet loading
Plane from point and normal vector with additional point in the plane. In additional to the point $\color{red}{P}$ (in red) and the normal vector $\color{green}{\vc{n}}$ (in green) that determine the plane, there is another point $Q$ (in yellow) that is constrained to lie in the plane. The vector from $P$ to $Q$ is shown in cyan. You can move the points $P$ and $Q$ and the vector $\vc{n}$ by dragging them with the mouse. Dragging the mouse elsewhere rotates the whole figure.
If the point represented by $\vc{x}$ is in the plane, the vector $\vc{x}-\vc{a}$ must be parallel to the plane, hence perpendicular to the normal vector $\vc{n}$. Two vectors are perpendicular if their dot product is zero. We conclude that for any point represented by $\vc{x}$ that is in the plane, the following equation must be satisfied: \begin{align*} \vc{n} \cdot (\vc{x}-\vc{a})=0. \end{align*} This is the equation for the plane perpendicular to $\vc{n}$ that goes through the point represented by $\vc{a}$.
Plane determined by three points
We just determined that to write the equation for a plane, we want a point $P$ in the plane and a normal vector $\vc{n}$. But most of us know that three points determine a plane (as long as they aren't collinear, i.e., lie in straight line). Here is a plane determined by three such points.
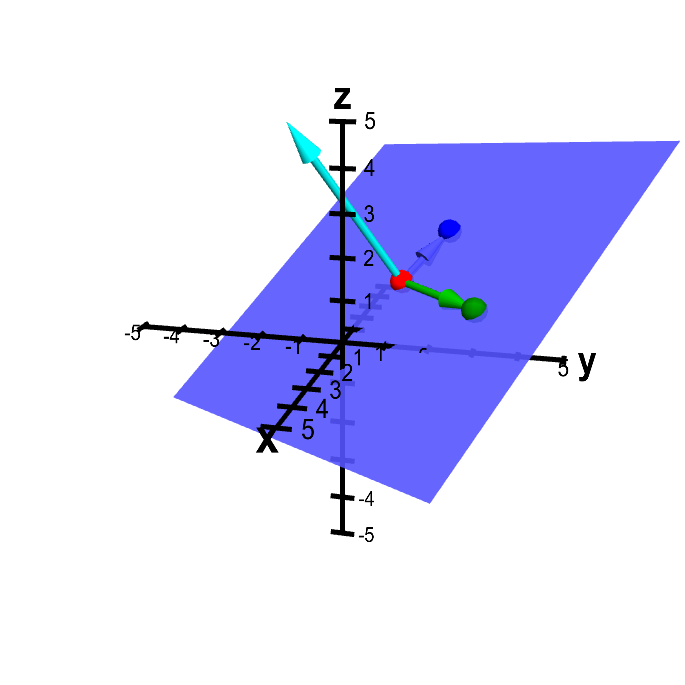
Applet loading
Plane determined from three points. The plane is determined by the points $\color{red}{P}$ (in red), $\color{green}{Q}$ (in green), and $\color{blue}{R}$ (in blue), which you can move by dragging with the mouse. The vectors from $\color{red}{P}$ to both $\color{green}{Q}$ and $\color{blue}{R}$ are drawn in the corresponding colors. The normal vector (in cyan) is the cross product of the green and blue vectors.
Since a plane is given by a point (say $\color{red}{P}$) and normal vector, somehow the addition of two points (say, $\color{green}{Q}$ and $\color{blue}{R}$ must determine the normal vector. Following the above logic, the normal vector must be perpendicular to the vector from $\color{red}{P}$ to $\color{green}{Q}$ and the vector from $\color{red}{P}$ to $\color{blue}{R}$. One way to obtain a vector perpendicular to two vectors is take their cross product. The normal vector in the above applet is indeed the cross product of those two vectors.
In summary, if you are given three points, you can take the cross product of the vectors between two pairs of points to determine a normal vector $\vc{n}$. Pick one of the three points, and let $\vc{a}$ be the vector representing that point. Then, the same equation described above, \begin{align*} \vc{n} \cdot (\vc{x}-\vc{a})=0. \end{align*} is the equation for the plane going through the three points.
If you find yourself in a position where you want to find the equation for a plane, look for a way to determine both a normal vector $\vc{n}$ and a point $\vc{a}$ through the plane. Then, you can simply use the above equation. You can see some examples for finding the equation of a plane.
Thread navigation
Vector algebra
- Previous: Parametrization of a line examples
- Next: Forming plane examples