Math Insight

Parametrization of a plane

A plane is determined by a point $\vc{p}$ in the plane and two vectors $\vc{a}$ and $\vc{b}$ parallel to the plane. (This is identical to the case with three points in the plane. Why?)

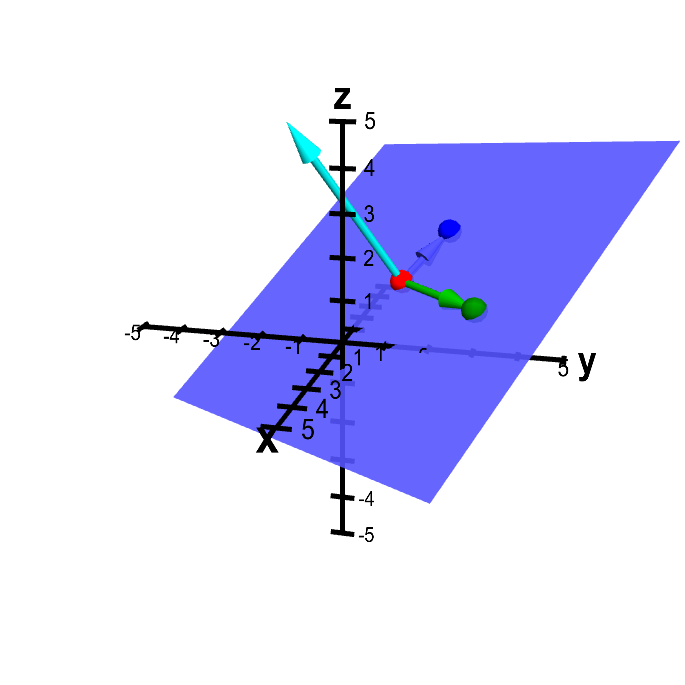
Applet loading

Plane determined from three points. The plane is determined by the points $\color{red}{P}$ (in red), $\color{green}{Q}$ (in green), and $\color{blue}{R}$ (in blue), which you can move by dragging with the mouse. The vectors from $\color{red}{P}$ to both $\color{green}{Q}$ and $\color{blue}{R}$ are drawn in the corresponding colors. The normal vector (in cyan) is the cross product of the green and blue vectors.

More information about applet.

From this fact, we can parametrize a plane just like we parametrized a line (only we'll need two parameters instead of one). If $\vc{x}$ is a point in the plane, the vector from $\vc{p}$ to $\vc{x}$ (i.e., $\vc{x}-\vc{p}$) is some multiple of $\vc{a}$ plus some multiple of $\vc{b}$. (Can you see why?) We can express this as $\vc{x}-\vc{p} = s\vc{a} + t\vc{b}$ for $t,s \in \vc{R}$. Usually, we'll write this as $\vc{x} = \vc{p} + s\vc{a} + t \vc{b}$. The real numbers $s$ and $t$ are the parameters for this parametrization of the line plane.

The idea of the parametrization is that as the parameters $s$ and $t$ sweep through all real numbers, the point $\vc{x}$ sweeps out the plane. In other words, it is a two-dimensional analogue of the parametrization of the line.

Here we've added the point $\vc{x}$ in cyan. You can move $\vc{x}$ directly or by changing the parameters $s$ and $t$ (the points on sliders).

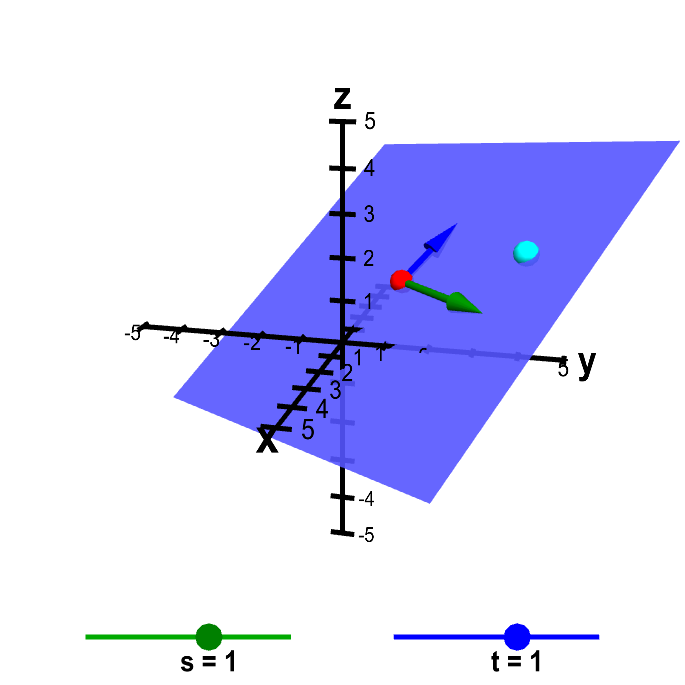
Applet loading

Parametrization of a plane. The plane is determined by the point $\color{red}{\vc{p}}$ (in red) and the vectors $\color{green}{\vc{a}}$ (in green) and $\color{blue}{\vc{b}}$ (in blue), which you can move by dragging with the mouse. The point $\vc{x} = \vc{p} + s\vc{a} + t \vc{b}$ (in cyan) sweeps out all points in the plane as the parameters $s$ and $t$ sweep through their values. You can move the cyan point $\vc{x}$ either by changing the values of $s$ and $t$ with the sliders or by moving the point directly (which updates the values of $s$ and $t$). For this applet, the values of $s$ and $t$ are restricted to be between -5 and 5, which restricts the possible locations of the cyan point, depending on the values of $\vc{a}$ and $\vc{b}$.

More information about applet.

Clearly, for any value of $s$ and $t$, the point $\vc{x}$ lies on the plane. Also, by changing $s$ and $t$, you can move the point $\vc{x}$ to any position on the plane (subject to the restriction of the applet that keeps $s$ and $t$ between -5 and 5).

You can see an example of parametrizing a plane here.