Polar coordinates
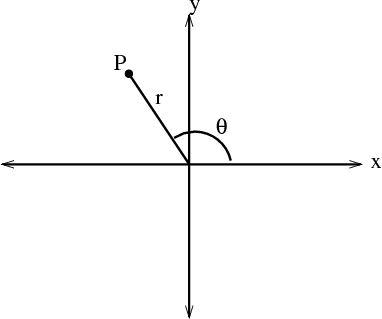
In two dimensions, the Cartesian coordinates $(x,y)$ specify the location of a point $P$ in the plane. Another two-dimensional coordinate system is polar coordinates. Instead of using the signed distances along the two coordinate axes, polar coordinates specifies the location of a point $P$ in the plane by its distance $r$ from the origin and the angle $\theta$ made between the line segment from the origin to $P$ and the positive $x$-axis. The polar coordinates $(r,\theta)$ of a point $P$ are illustrated in the below figure.
As $r$ ranges from 0 to infinity and $\theta$ ranges from 0 to $2\pi$, the point $P$ specified by the polar coordinates $(r,\theta)$ covers every point in the plane. Adding $2\pi$ to $\theta$ brings us back to the same point, so if we allowed $\theta$ to range over an interval larger than $2\pi$, each point would have multiple polar coordinates. Hence, we typically restrict $\theta$ to be in the interal $0 \le \theta < 2\pi$. However, even with that restriction, there still is some non-uniqueness of polar coordinates: when $r=0$, the point $P$ is at the origin independent of the value of $\theta$.
The following applet allows you to explore how changing the polar coordinates $r$ and $\theta$ moves the point $P$ around the plane. You change the polar coordinates using sliders and observe how the point moves in the Cartesian plane. You can also move the point in the Cartesian plane and observe how the polar coordinates change. Notice the non-uniqueness of polar coordinates when $r=0$.
Conversion formulas
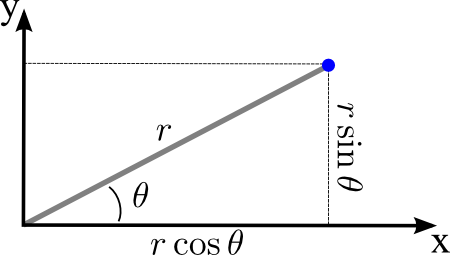
We can calculate the Cartesian coordinates of a point with polar coordinates $(r,\theta)$ by forming the right triangle illustrated in the below figure. The hypotenuse is the line segment from the origin to the point, and its length is $r$. The projection of this line segment on the $x$-axis is the leg of the triangle adjacent to the angle $\theta$, so $x=r\cos\theta$. The $y$-component is determined by the other leg, so $y=r\sin\theta$. Our conversion formula is \begin{align} x &= r\cos\theta\notag\\ y &= r\sin\theta. \label{polar_to_cartesian} \end{align}
To go the other direction, one can use the same right triangle. Since $r$ is the distance from the origin to $(x,y)$, it is the magnitude $r=\sqrt{x^2+y^2}$. Alternatively, from the equation \eqref{polar_to_cartesian}, one can calculate directly that \begin{align*} x^2+y^2 &=r^2\cos^2\theta+r^2\sin^2\theta\\ &= r^2(\cos^2\theta+\sin^2\theta)=r^2. \end{align*}
Taking the ratio of $y$ and $x$ from equation \eqref{polar_to_cartesian}, one can obtain a formula for $\theta$, \begin{align*} \frac{y}{x} &= \frac{r\sin\theta}{r \cos\theta} = \tan\theta. \end{align*} One can also see this relationshp from the above right triangle. We can set $\theta= \arctan \frac{y}{x}$, but a problem is that $\arctan$ gives a value between $-\pi/2$ and $\pi/2$. One might neet to add $\pi$ or $2\pi$ to get the correct angle. With this caveat (and also mapping points where $x=0$ to $\theta=\pi/2$ or $-\pi/2$), one obtains the following formula to convert from Cartesian to polar coordinates \begin{align} r &= \sqrt{x^2+y^2}\notag\\ \theta &= \arctan \frac{y}{x}. \end{align}
What about the point where $(x,y)=(0,0)$? In this case, the angle $\theta$ isn't well defined. You could just take it to be $\theta=0$ to be concrete.
Another perspective on polar coordinates
In the above applet, we represented polar coordinates by two separate points on a $r$-axis and a $\theta$-axis (the two sliders). We could also put those two axes together into a single $(r,\theta)$ plane (just like the $(x,y)$ plane of Cartesian coordinates). This simple change of representing the polar coordinates as a single point on the polar $(r,\theta)$ plane is reflected in the following applet. Such a slight shift in perspective has more consequences than you might imagine, as you can read about in a page about polar coordinates as a mapping from the $(r,\theta)$ plane to the $(x,y)$ plane.
