Cartesian coordinates
Cartesian coordinates allow one to specify the location of a point in the plane, or in three-dimensional space. The Cartesian coordinates (also called rectangular coordinates) of a point are a pair of numbers (in two-dimensions) or a triplet of numbers (in three-dimensions) that specified signed distances from the coordinate axis.
Cartesian coordinates of the plane
The Cartesian coordinates in the plane are specified in terms of the $x$ coordinates axis and the $y$-coordinate axis, as illustrated in the below figure. The origin is the intersection of the $x$ and $y$-axes. The Cartesian coordinates of a point in the plane are written as $(x,y)$. The first number $x$ is called the $x$-coordinate (or $x$-component), as it is the signed distance from the origin in the direction along the $x$-axis. The $x$-coordinate specifies the distance to the right (if $x$ is positive) or to the left (if $x$ is negative) of the $y$-axis. Similarly, the second number $y$ is called the $y$-coordinate (or $y$-component), as it is the signed distance from the origin in the direction along the $y$-axis, The $y$-coordinate specifies the distance above (if $y$ is positive) or below (if $y$ is negative) the $x$-axis. The following figure, the point has coordinates $(-3,2)$, as the point is three units to the left and two units up from the origin.
The below applet illustrates the Cartesian coordinates of a point in the plane. It's similar to the above figure, only it allows you to change the point.
Cartesian coordinates in the plane. The Cartesian coordinates $(x,y)$ of the blue point specify its location relative to the origin, which is the intersection of the $x$- and $y$-axis. You can change the location of the point by dragging it with your mouse.
Cartesian coordinates of three-dimensional space
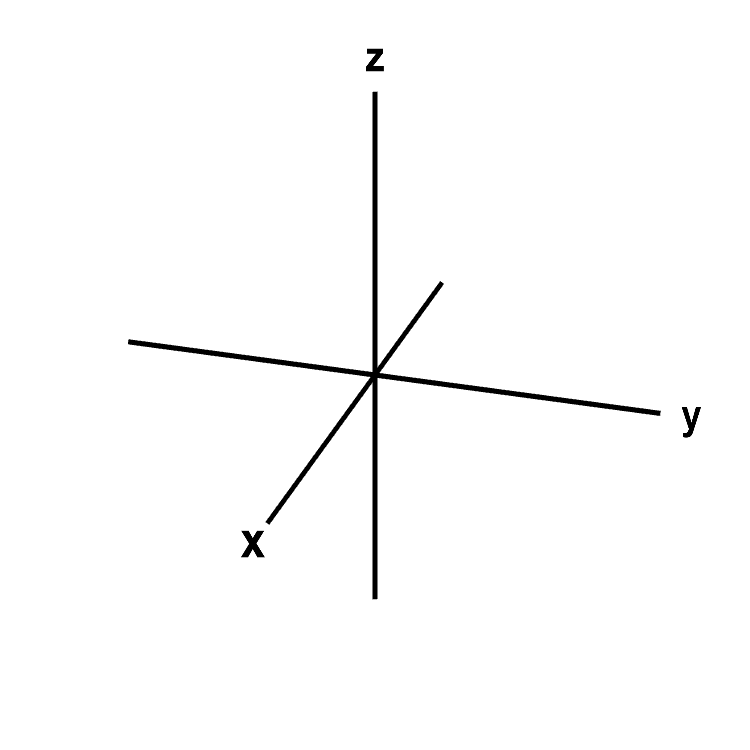
In three-dimensional space, the Cartesian coordinate system is based on three mutually perpendicular coordinate axes: the $x$-axis, the $y$-axis, and the $z$-axis, illustrated below. The three axes intersect at the point called the origin. You can imagine the origin being the point where the walls in the corner of a room meet the floor. The $x$-axis is the horizontal line along which the wall to your left and the floor intersect. The $y$-axis is the horizontal line along which the wall to your right and the floor intersect. The $z$-axis is the vertical line along which the walls intersect. The parts of the lines that you see while standing in the room are the positive portion of each of the axes, illustrated by the halves of the each axis labeled by $x$, $y$, and $z$ in the below applet. The negative part of these axes would be the continuations of the lines outside of the room, illustrated by the unlabeled halves of each axis, below.
Applet loading
Three-dimensional Cartesian coordinate axes. A representation of the three axes of the three-dimensional Cartesian coordinate system. The positive $x$-axis, positive $y$-axis, and positive $z$-axis are the sides labeled by $x$, $y$ and $z$. The origin is the intersection of all the axes. The branch of each axis on the opposite side of the origin (the unlabeled side) is the negative part. You can drag the figure with the mouse to rotate it.
With above definitions of the positive $x$, $y$, and $z$-axis, the resulting coordinate system is called right-handed; if you curl the fingers of your right hand from the positive $x$-axis to the positive $y$-axis, the thumb of your right hand points in the direction of the positive $z$-axis. Switching the locations of the positive $x$-axis and positive $y$-axis creates left-handed coordinate system. The right-handed and left-handed coordinate systems represent two equally valid mathematical universes. The problem is that switching universes will change the sign on some formulas. Since these pages are written in the right-handed universe, we suggest you live in our universe while studying from these pages.
In addition to the three coordinate axes, we often refer to three coordinate planes. The $xy$-plane is the horizontal plane spanned by the $x$ and $y$-axes. It is identical to the two-dimensional coordinate plane and contains the floor in the room analogy. Similarly, the $xz$-plane is the vertical plane spanned by the $x$ and $z$-axes and contains the left wall in the room analogy. Lastly, the $yz$-plane is the vertical plane spanned by the $y$ and the $z$-axis and contains the right wall in the room analogy.
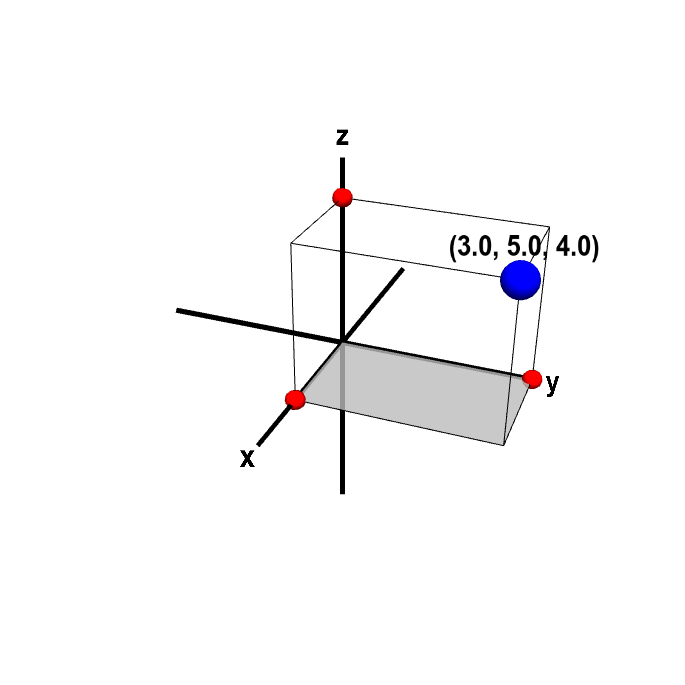
The Cartesian coordinates of a point in three dimensions are a triplet of numbers $(x,y,z)$. The three numbers, or coordinates, specify the signed distance from the origin along the $x$, $y$, and $z$-axes, respectively. They can be visualized by forming the box with edges parallel to the coordinate axis and opposite corners at the origin and the given point, as illustrated in the following applet.
Applet loading
Cartesian coordinates of a point in three dimensions. The Cartesian coordinates $(x,y,z)$ of a point in three-dimensions specify the signed distance from the origin along the $x$, $y$, and $z$-axes, respectively. The rectangular box has opposite corners at the origin and at the blue point. The three coordinates of the blue point are represented by the red points, which are the corners of the box along each axis. You can change the point by dragging the blue point with the mouse. Alternatively, you can independently change one of the coordinates by dragging a red point.
Given the above corner-of-room analogy, we could form the Cartesian coordinates of the point at the top of your head, as follows. Imagine that you are two meters tall, and that you walk four meters from the origin along the $x$-axis, then turn left and walk parallel to the $y$-axis three meters into the room. The Cartesian coordinates of the point at the top of your head would be $(4,3,2)$.
Unlike other coordinate systems, such as spherical coordinates, Cartesian coordinates specify a unique point for every pair $(x,y)$ or triple $(x,y,z)$ of numbers, and each coordinate can take on any real value.
Vectors and higher dimensions
Cartesian coordinates can be used not only to specify the location of points, but also to specify the coordinates of vectors. The Cartesian coordinates of two or three-dimensional vectors look just like those of points in the plane or three-dimensional space.
But, there is no reason to stop at three-dimensions. We could define vectors in four, five, or higher dimensions by just specifying four, five, or more Cartesian coordinates. We can't visualize these higher dimensions like we did with the above applets, but we can easily write down the list of numbers for the coordinates. You can check out examples of n-dimensional vectors to convince yourself that talking about higher dimensions isn't completely crazy.
Similar pages
- Spherical coordinates
- Lines (and other items in Analytic Geometry)
- Polar coordinates
- Cylindrical coordinates
- Polar coordinates mapping
- Parametrization of a line
- Parametrization of a line examples
- Vectors in two- and three-dimensional Cartesian coordinates
- The elliptic paraboloid
- The hyperbolic paraboloid
- More similar pages
