Parametrization of a line
A line is determined by two points $\color{red} P$ and $\color{green} Q$. The following applet illustrates this simple idea. You can change the position of the line by moving the red or the green point with the mouse. Dragging with the mouse elsewhere rotates the picture.
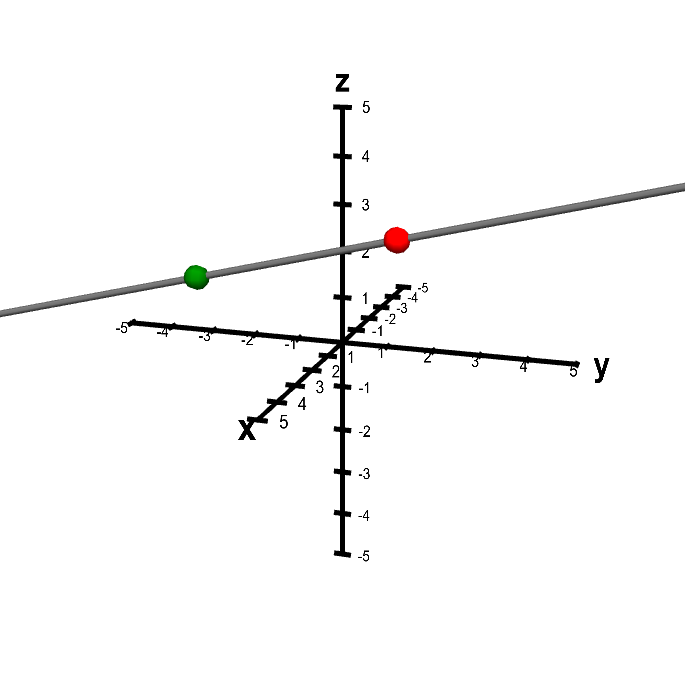
Applet loading
A line determined by two points. The position of the thick gray line is determined by the red and green points, which you can move by dragging them with the mouse. If you drag elsewhere in the figure, the whole figure rotates. Rotating the figure can help give a three-dimensional perspective.
We want to write an equation for the line. However, since we are in three dimensions, we can't write a single equation like $y=2x-3$ to describe the line. (If you don't believe this statement, check out this page.) Instead, we'll write a parametrization for the line.
Before we continue, let's to change our perspective about the line. First, rather than thinking of a line being determined by two points, we'll think of it as being determined by a point $\color{red} P$ and a vector $\color{green}{\vc{v}}$ parallel to the line. (The vector $\color{green}{\vc{v}}$ could simply be the vector from the point $\color{red} P$ to the point $\color{green} Q$.)
Second, we'll think of the point $\color{red} P$ as the endpoint of a vector $\color{red}{\vc{a}}$ with tail at the origin. We could visualize the new perspective with the following applet. It's essentially identical to the above applet, except that I've drawn in the vectors mentioned above. You can drag the tips of the vectors to change the line.
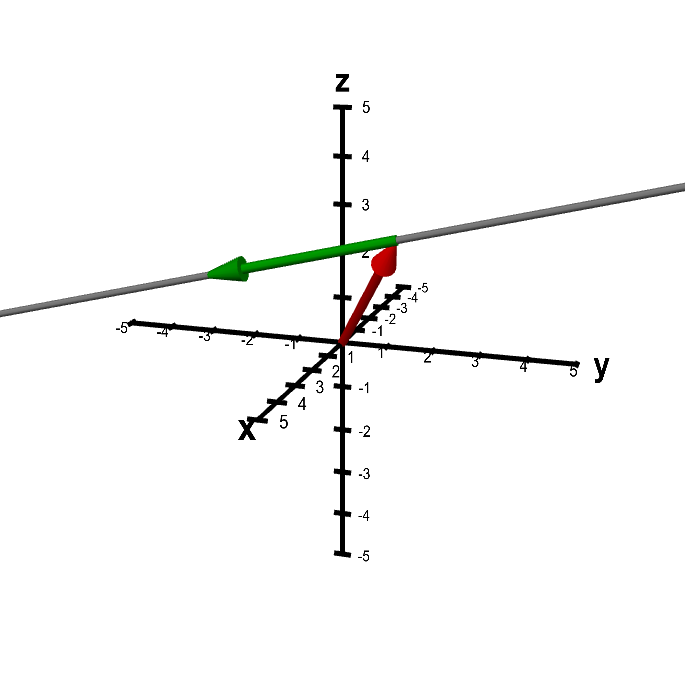
Applet loading
A line determined by two vectors. The position of the thick gray line is determined by the red and green vectors, as it is constrained to pass through the endpoint of the red vector and to be parallel to the green vector. You can move the vectors by dragging their tips with the mouse. If you drag elsewhere in the figure, the whole figure rotates. Rotating the figure can help give a three-dimensional perspective.
Now we are ready to derive a condition for a point $\color{blue}{\vc{x}}$ being on the line determined by $\color{red}{\vc{a}}$ and $\color{green}{\vc{v}}$. We represent a point $\color{blue}{\vc{x}}$ on the line by the vector $\color{blue}{\vc{x}}$ pictured in blue in the below applet. (We will refer to the point $\color{blue}{\vc{x}}$ as being the endpoint of the vector $\color{blue}{\vc{x}}$ when its tail is fixed at the origin.) By the definition of our line, the point $\color{blue}{\vc{x}}$ is on the line if the vector from $\color{red}{\vc{a}}$ to $\color{blue}{\vc{x}}$ (i.e, $\color{cyan}{\vc{x}-\vc{a}}$, pictured in cyan below) is parallel to $\color{green}{\vc{v}}$ (in green).
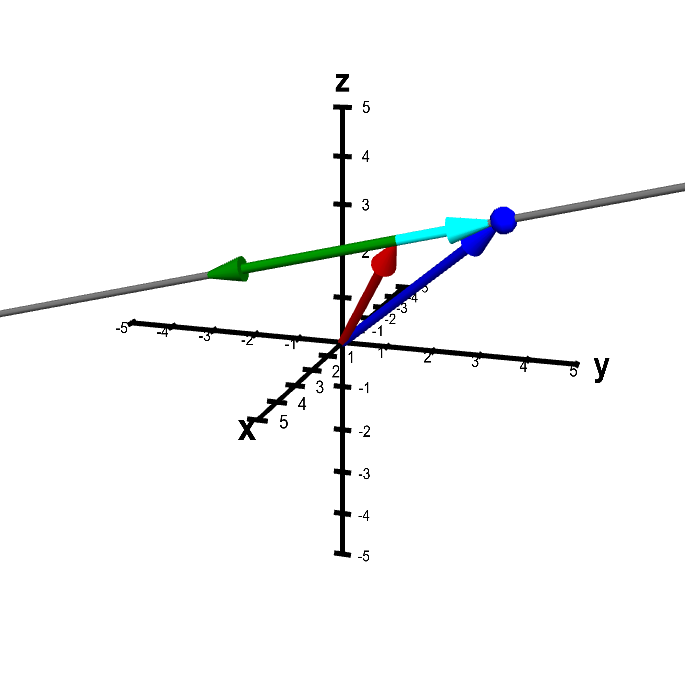
Applet loading
A point on the line determined by two vectors. The point $\color{blue}{\vc{x}}$ (represented by the blue point as well as the blue vector) is constrained to be on the line passing through the point $\color{red}{\vc{a}}$ (represented by the red vector) and parallel to the vector $\color{green}{\vc{v}}$ (in green). You can move $\color{blue}{\vc{x}}$ by dragging it with the mouse, but it is constrained to be on the line. You can change the line by dragging $\color{red}{\vc{a}}$ or $\color{green}{\vc{v}}$ with the mouse. Since $\color{blue}{\vc{x}}$ is on the line, the vector $\color{green}{\vc{v}}$ is always parallel to the vector $\color{cyan}{\vc{x}-\vc{a}}$ (in cyan).
What does it mean for two vectors to be parallel? (Note that we use the term “parallel” to include what you might think of as anti-parallel, meaning pointing in opposite directions.) Two vectors are parallel if one vector can be expressed as a scalar multiple of the other. So, $\color{cyan}{\vc{x}-\vc{a}}$ is parallel to $\color{green}{\vc{v}}$ if and only if $\color{cyan}{\vc{x}-\vc{a}} = t \color{green}{\vc{v}}$ for some $t \in \vc{R}$. We usually write this condition for $\vc{x}$ being on the line as $$\vc{x} = t \vc{v} + \vc{a}.$$ This equation is called the parametrization of the line, where $t$ is a free parameter that is allowed to be any real number.
The idea of the parametrization is that as the parameter $t$ sweeps through all real numbers, $\vc{x}$ sweeps out the line. In the last applet on this page, we've changed the perspective so that now you control $t$ by moving the point on the slider. To make visualization a little easier, we show only the endpoints of the vectors $\vc{a}$ and $\vc{x}$.
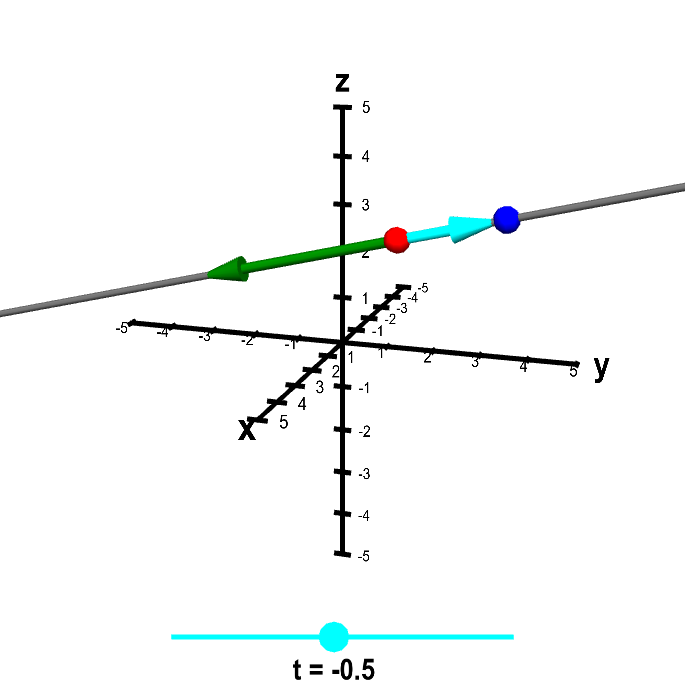
Applet loading
Line parametrization. The blue point $\color{blue}{\vc{x}}$ sweeps out the line parameterized by $\color{blue}{\vc{x}} = \color{red}{\vc{a}} + t\color{green}{\vc{v}}$, where $\color{red}{\vc{a}}$ is the red point and $\color{green}{\vc{v}}$ is the green vector. Change the line by dragging the red point or green arrow heads. Change the position of $\color{blue}{\vc{x}}$ along the line by dragging either the point itself or the cyan dot on the slider that determines the value of $t$. Dragging elsewhere on the figure rotates the graph. Notice that when $t=0$, then $\color{blue}{\vc{x}}=\color{red}{\vc{a}}$. And when $t=1$, $\color{blue}{\vc{x}}$ is on top of the endpoint of the vector $\color{green}{\vc{v}}$, which is at position $\color{red}{\vc{a}}+\color{green}{\vc{v}}$.
If you want to read something more concrete about line parametrization, you can see examples of finding the parametrization of a line.
Thread navigation
Math 2374
Vector algebra
Similar pages
- Parametrization of a line examples
- Lines (and other items in Analytic Geometry)
- A line or a plane or a point?
- Intersecting planes example
- An introduction to parametrized curves
- Derivatives of parameterized curves
- Tangent lines to parametrized curves
- Tangent line to parametrized curve examples
- Parametrized curve and derivative as location and velocity
- Line integrals are independent of parametrization
- More similar pages