Applet: A differentiable function with discontinuous partial derivatives
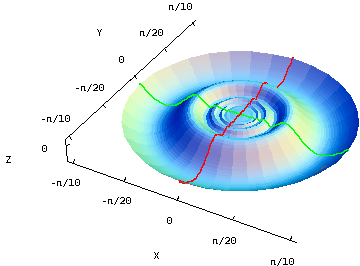
The function $$f(x,y)=\begin{cases}(x^2+y^2)\sin\left(\frac{1}{\sqrt{x^2+y^2}}\right) & \text{ if $(x,y) \ne (0,0)$}\\0 & \text{ if $(x,y) = (0,0)$}\end{cases}$$ is differentiable even at the origin. You can see this because $f(x,y)$ is squeezed between the two elliptic paraboloids $z=x^2+y^2$ and $z=-x^2-y^2$, both of which share the horizontal tangent plane $z=0$ at the origin.
The cross sections $x=0$ (in red) and $y=0$ (in green) also highlight the how the graph flattens out and stays differentiable at the origin despite the rapid oscillations of the sinusoid. You can press “F” when your mouse is over the graph to remove the “faces” composing the surface and see the cross sections in isolation.
The partial derivatives at the origin are zero, as they must be given the horizontal tangent plane. (You have to use the limit definition to calculate them.) The partial derivatives oscillate wildly as one approaches the origin, getting arbitrarily close to both 1 and $-1$ within any neighborhood of the origin. Therefore, the partial derivatives are discontinuous at the origin.
This function provides a counterexample showing that partial derivatives do not need to be continuous for a function to be differentiable, demonstrating that the converse of the differentiability theorem is not true.
Applet file: differentiable_function_discontinuous_partial_derivatives.lg3d
Applet links
This applet is found in the pages
General information about LiveGraphics3D applets
This applet was created using LiveGraphics3D. To manipulate it, you can
- click and drag to rotate in any direction,
- shift + click and drag up/down to zoom out/in,
- shift + click and drag left/right to rotate around an axis coming out of the screen, and
- press Home to reset to the original view.
Most of the LiveGraphics3D applets have parameters that you can change. In general, you can click and drag points or balls around to change the parameters.
Since these applets use Java, you must have Java installed and properly configured in your browser for the them to display. You can get Java here. If you have trouble getting them to display in your browser, you can visit the LiveGraphics3D troubleshooting page for information on how to get the Java applets to work.
On occasion, even when Java is configured correctly, the Java applets don't load the first time and one instead sees an error message. You can wait a few moments to see if the applet will eventually load itself anyway. You can also reload the page to see if the applet will properly load. Sometimes, one needs to do this multiple times.