A differentiable function with discontinuous partial derivatives
The differentiability theorem states that continuous partial derivatives are sufficient for a function to be differentiable. It's important to recognize, however, that the differentiability theorem does not allow you to make any conclusions just from the fact that a function has discontinuous partial derivatives. The converse of the differentiability theorem is not true. It is possible for a differentiable function to have discontinuous partial derivatives.
An example of such a strange function is $$f(x,y)=\begin{cases}(x^2+y^2)\sin\left(\frac{1}{\sqrt{x^2+y^2}}\right) & \text{ if $(x,y) \ne (0,0)$}\\0 & \text{ if $(x,y) = (0,0)$}.\end{cases}$$ Since the argument of the sinusoid approaches infinity as one approaches the origin, it oscillates wildy near the origin. But, the sinusoid is bounded between $-1$ and 1, and the oscillations of the sinusoid are tempered by the quadratic term $x^2+y^2$. The function is squeezed between two elliptic paraboloids $z=x^2+y^2$ and $z=-x^2-y^2$ that go to zero very quickly as one approaches the origin. As both paraboloids have the same horizontal tangent plane at the origin $z=0$, we can infer that $f(x,y)$ has the same tangent plane at the origin. The function $f(x,y)$ is differentiable at the origin.
The below graph of $f(x,y)$ shows how it flattens near the origin. The cross sections facilitate visualizing its horizontal tangent plane.
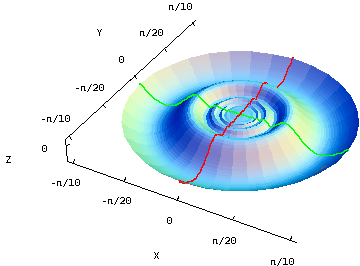
A differentiable function with discontinuous partial derivatives. Although this function contains a wildly oscillating sinusoidal component, these oscillations are flattened out at the origin. The function does have a horizontal tangent plane at the origin, i.e., it is differentiable there. The cross sections $x=0$ (in red) and $y=0$ (in green) highlight the how the graph flattens out and stays differentiable at the origin despite the rapid oscillations of the sinusoid. You can press “F” when your mouse is over the graph to remove the “faces” composing the surface and see the cross sections in isolation. Although the function is differentiable, its partial derivatives oscillate wildly near the origin, creating a discontinuity there. This function provides a counterexample showing that partial derivatives do not need to be continuous for a function to be differentiable, demonstrating that the converse of the differentiability theorem is not true.
To verify that the partial derivatives of $f$ are zero at the origin, consistent with the horizontal tangent plane, one must use the limit definition. For example, the derivative with respect to $x$ can be calculated by \begin{align*} \pdiff{f}{x}(0,0) &= \lim_{h \to 0} \frac{f(h,0)-f(0,0)}{h}\\ &= \lim_{h \to 0}\frac{h^2 \sin (1/|h|)-0}{h} \\ &= \lim_{h \to 0}h \sin (1/|h|) =0. \end{align*} A similar calculation shows that $\pdiff{f}{y}(0,0)=0$.
Away from the origin, one can use the standard differentiation formulas to calculate that \begin{align*} \pdiff{f}{x}(x,y) &= 2 x \sin \left(\frac{1}{\sqrt{x^2+y^2}}\right)-\frac{x \cos \left(\frac{1}{\sqrt{x^2+y^2}}\right)}{\sqrt{x^2+y^2}}\\ \pdiff{f}{y}(x,y) &= 2 y \sin \left(\frac{1}{\sqrt{x^2+y^2}}\right)-\frac{y \cos \left(\frac{1}{\sqrt{x^2+y^2}}\right)}{\sqrt{x^2+y^2}}. \end{align*} Both of these derivatives oscillate wildly near the origin. For example, the derivative with respect to $x$ along the $x$-axis is $$\pdiff{f}{x}(x,0) = 2 x \sin \left(1/|x|\right)-\text{sign}(x) \cos \left(1/|x|\right),$$ for $x \ne 0$, where $\text{sign}(x)$ is $\pm 1$ depending on the sign of $x$. In this case, the sine term goes to zero near the origin but the cosine term oscillates rapidly between 1 and $-1$, as it is not multiplied by anything small. As $\pdiff{f}{x}$ approaches both 1 and $-1$ within any neighborhood of the origin, it is discontinuous there. In the same way, one can show that $\pdiff{f}{y}$ has wild oscillations and is discontinuous at the origin.
This function is a cautionary tale, reminding you to read your theorems carefully so as not to jump to conclusions. Although counterexamples such as these are strange functions, studying them can help you understand more precisely what your mathematics is telling you. This function should prevent you from misinterpreting the differentiability theorem, as you now know that continuous partial derivatives imply differentiability but not vice-versa.
Thread navigation
Multivariable calculus
- Previous: Non-differentiable functions must have discontinuous partial derivatives
- Next: Introduction to the multivariable chain rule
Math 2374
Similar pages
- The multidimensional differentiability theorem
- Non-differentiable functions must have discontinuous partial derivatives
- Introduction to differentiability in higher dimensions
- Subtleties of differentiability in higher dimensions
- The derivative matrix
- An introduction to the directional derivative and the gradient
- Introduction to partial derivatives
- Partial derivative examples
- Partial derivative by limit definition
- The multivariable linear approximation
- More similar pages