Math Insight

Solutions to elementary derivative problems

The following is a set of solutions to the elementary derivative problems.

Problem 1

  1. $\diff{h}{p}$ is
    1. negative for $-3.5 < p < -2$, $0 < p < 1$, and $1 < p < 2$.
    2. positive for $p < -3.5$, $-2 < p < 0$, and $p > 2$.
    3. zero for $p=-2$, $p=0$, and $p=2$.
    4. undefined for $p=-3.5$ and $p=1$.
  2. Critical points are all the points where $\diff{h}{p}$ is zero or undefined. Critical points are $p=-3.5$, $p=-2$, $p=0$, $p=1$, and $p=2$.
  3. $\diffn{h}{p}{2}$
    1. negative for $-1 < p < 1$
    2. positive for $-3.5 < p < -1$ and $p > 1$.
    3. zero for $p < -3.5$ and $p=-1$.
    4. undefined for $p=-3.5$ and $p=1$.
  4. The inflection points are the point in the domain of the function where $\diffn{h}{p}{2}$ changes sign. They are at $p=-1$ and $p=1$.

Problem 2

  1. $r'(z)$
    1. is negative for $z < -2$, $-2 < z < -1$, $-1 < z < -1/2$, and $1/2 < z < 2$.
    2. positive for $-1/2 < z < 1/2$, $2 < z < 3$, and $z > 3$.
    3. zero for $z=-1/2$, $z=1/2$, and $z=2$.
    4. undefined for $z=-2$, $z=-1$, and $z=3$.
  2. Critical points are $z=-2$, $z=-1$, $z=-1/2$, $z=1/2$, $z=2$, and $z=3$.
  3. $r''(z)$ is
    1. negative for $z < -2$ and $0 < z < 1$.
    2. positive for $-2 < z < -1$, $-1 < z < 0$, $1 < z < 3$, and $z > 3$
    3. zero for $z=0$ and $z=1$.
    4. undefined for $z=-2$, $z=-1$, and $z=3$
  4. Inflection points are $z=-2$, $z=0$, and $z=1$.

Problem 3

The critical points are labeled by the red open circles, the inflection points by the dark green open diamonds. The intervals where the derivative is positive and negative are indicated by the thin and thick purple lines labeled “increasing” and “decreasing,” respectively. The intervals where the second derivative is positive and negative are indicated by the thin and thick blue lines labeled “concave up” and “concave down,” respectively. The derivative is graphed by the green curve.

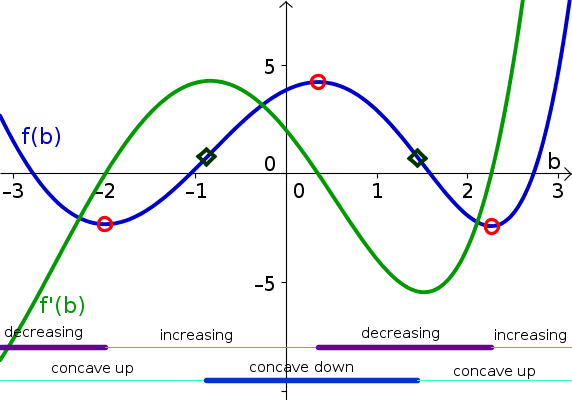
Derivative example function 3, with derivative

Problem 4

The critical points are labeled by the red open circles, the inflection points by the dark green open diamonds. The intervals where the derivative is positive and negative are indicated by the thin and thick purple lines, respectively. The intervals where the second derivative is positive and negative are indicated by the thin and thick blue line, respectively. The derivative is graphed by the green curve.

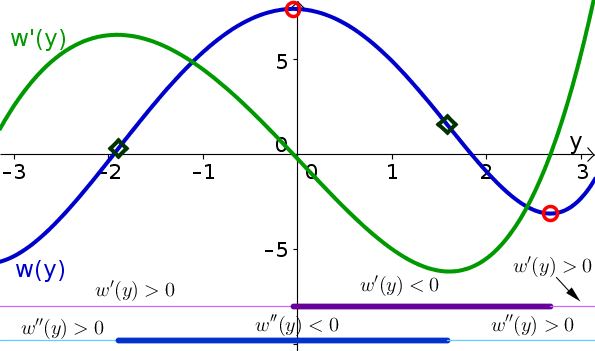
Derivative example function 4, with derivative

Problem 5

The critical points are labeled by the red open circles, and the derivative is not defined at the points. Also, along the horizontal line shown in red, the derivative is zero, so these are critical points. The second derivative is zero everywhere it is defined, which is everywhere except at the red circles. The intervals where the derivative is positive and negative are indicated by the thin and thick purple lines, respectively. The derivative is graphed by the green curve, which is constant along intervals and jumps between those intervals. The second derivative, as shown by the thick orange line, is zero everywhere it is defined. Although not shown by the thick orange line, it is not defined at the points above or below the red circles.

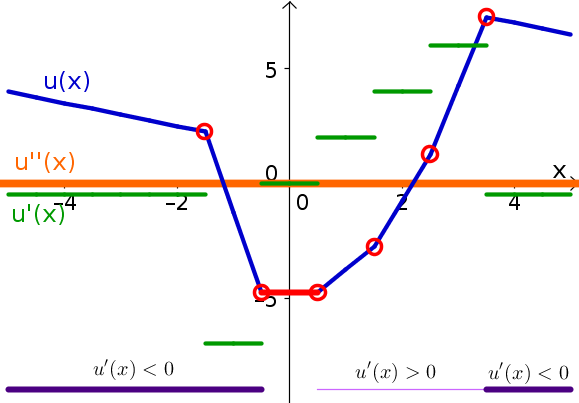
Derivative example function 5, with derivative

Problem 6

The linear approximation is the tangent line at $z=3$. Since $g(3)=5(3)^2-3+22 = 64$, $g'(z)=10z-1$, $g'(3)=10(3)-1 = 29$, the linear approximation is \begin{align*} L(z) = 64+29(z-3). \end{align*}

Problem 7

The tangent line is the same as the linear approximation of the previous problem. It is \begin{align*} L(z) = 64+29(z-3). \end{align*}

Problem 8

The linear approximation is the tangent line. By the product rule, \begin{align*} \diff{k}{q} &= \diff{q}{q}e^{-q} + q \diff{e^{-q}}{q}\\ &= 1 e^{-q} + q (-e^{-q})\\ &= (1-q)e^{-q} \end{align*} The linear approximation for $k$ around $q=a$ is \begin{align*} L(q) &= k(a) + k'(a)(q-a)\\ &= ae^{-a} + (1-a)e^{-a}(q-a) \end{align*}

This answer looks uglier than the original equation! However, the ugliness is only in its dependence on $a$, which is a fixed number. It depend on $q$ only linearly.

Problem 9

Using the chain rule, the derivative of $m$ is \begin{align*} m'(y) = 2ye^{y^2}. \end{align*} The equation for the tangent line at $y=b$ is \begin{align*} L(y) &= m(b) + m'(b)(y-b)\\ &= e^{b^2} + 2be^{b^2}(y-b). \end{align*} The dependence on $b$ isn't pretty, but the dependence on $y$ is simple.

Problem 10

By the product rule \begin{align*} x'(t) &= (t^3)'\ln(t) + t^3 (\ln(t))'\\ &= 3t^2 \ln(t) + t^3 \frac{1}{t}\\ &= 3t^2 \ln(t) + t^2. \end{align*}

The slope of the tangent line at $t=2$ is $x'(2) = 3 \cdot 2^2 \ln(2) + 2^2 = 12 \ln(2)+4$. At the point $t=\bigstar$, the slope is $x'(\bigstar) = 3 \bigstar^2 \ln(\bigstar) + \bigstar^2$.

Problem 11

  1. $\displaystyle\diff{y}{z} = a \frac{1}{az} = \frac{1}{z}$.
  2. $\displaystyle\diffn{y}{z}{2} = \diff{}{z} \frac{1}{z} = -\frac{1}{z^2}.$

Problem 12

  1. $z'(y)=bce^{by}$
  2. $z'(0)=bc$
  3. $z'(1/b) = bce^{b/b} = bce^{1}= bce$
  4. $z''(y) = b^2ce^{by}$
  5. $z''(0)=b^2c$
  6. $z''(1/b)= b^2ce^{b/b} = b^2ce^{1}=b^2ce$

Problem 13

  1. $h'(s)= (a^2+b^2)2se^{s^2}=2(a^2+b^2)se^{s^2}$
  2. $h'(1)= 2(a^2+b^2)e^{1}= 2(a^2+b^2)e$
  3. $h''(s) =2(a^2+b^2)(e^{s^2}+2s^2e^{s^2})= 2(a^2+b^2)(1+2s^2)e^{s^2}$
  4. $h''(1) = 2(a^2+b^2)(1+2)e^{1}= 6(a^2+b^2)e$

Problem 14

\begin{align*} s'(u) &= \frac{(1-u) (1+u)' - (1+u)(1-u)'}{(1-u)^2}\\ &= \frac{(1-u) 1 - (1+u)(-1)}{(1-u)^2}\\ &= \frac{2}{(1-u)^2} \end{align*}

Problem 15

\begin{align*} g'(x) &= (x^2)'e^{-x} + x^2 (e^{-x})'\\ &= 2x e^{-x} - x^2e^{-x}\\ &= (2x -x^2)e^{-x} \end{align*}

Problem 16

\begin{align*} f'(x) &= (x^n)'e^{-x} + x^n(e^{-x})'\\ &= n x^{n-1}e^{-x} -x^ne^{-x}\\ &= (nx^{n-1} - x^n)e^{-x} \end{align*}

Similar pages

See also