Math Insight

Elementary derivative problems

 

Problem 1

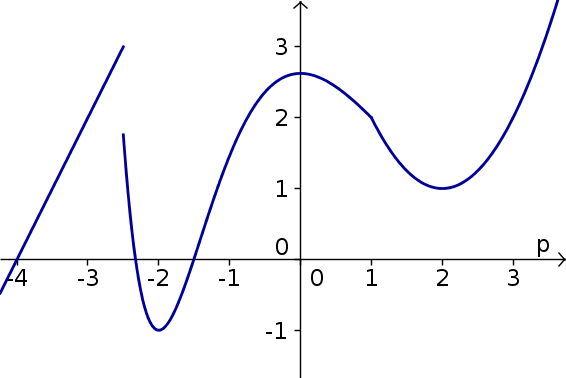
Below is a graph of the function $h(p)$.

  1. For what values of $p$ is $\diff{h}{p}$
    1. negative?
    2. positive?
    3. zero?
    4. undefined?
  2. Find all critical points of $h$.
  3. For what values of $p$ is $\diffn{h}{p}{2}$
    1. negative?
    2. positive?
    3. zero?
    4. undefined?
  4. Find all inflection points of $h$.
Derivative example function 1

Problem 2

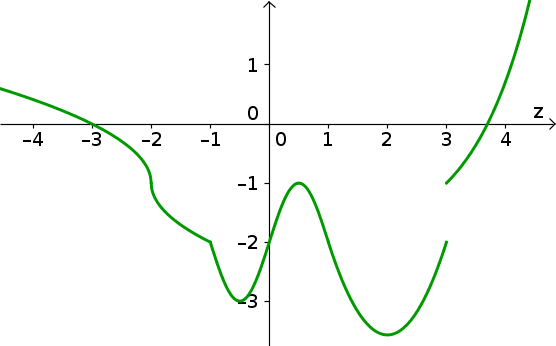
Below is a graph of the function $r(z)$.

  1. For what values of $z$ is $r'(z)$
    1. negative?
    2. positive?
    3. zero?
    4. undefined?
  2. Find all critical points of $r$.
  3. For what values of $z$ is $r''(z)$
    1. negative?
    2. positive?
    3. zero?
    4. undefined?
  4. Find all inflection points of $r$.
Derivative example function 2

Problem 3

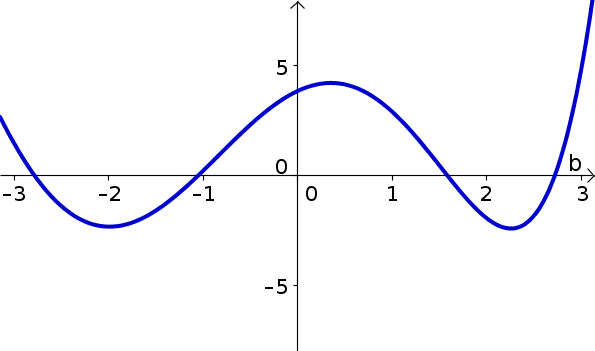
Let $f(b)$ be the function graphed below. Identify critical points, inflection points, and locations where the derivative and second derivative of $f$ are positive and negative. Use these results to graph $f'(b)$.

Derivative example function 3

Problem 4

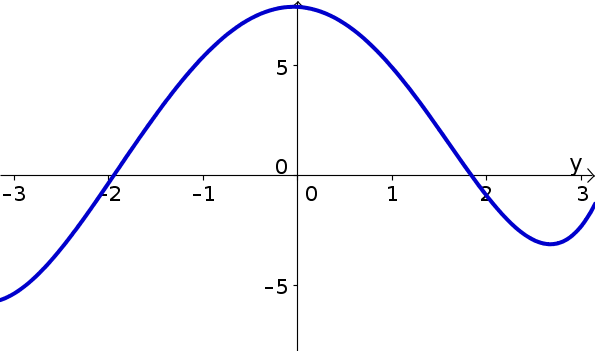
Let $w(y)$ be the function graphed below. Identify critical points, inflection points, and locations where the derivative and second derivative of $w$ are positive and negative. Use these results to graph $\diff{w}{y}$.

Derivative example function 4

Problem 5

Let $u(x)$ be the function graphed below. Identify critical points, inflection points, and locations where the derivative and second derivative of $u$ are positive and negative. Use these results to graph $\diff{u}{x}$ and $\diffn{u}{x}{2}$.

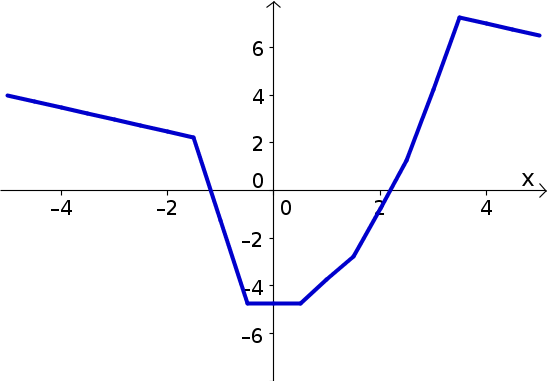
Derivative example function 5

Problem 6

Let $g(z)=5z^2-z+22$. Find a linear function that is a good approximation of $g$ for values of $z$ near $3$.

Problem 7

Let $g(z)=5z^2-z+22$. Find the equation for the tangent line to the graph of $g$ at the point $z=3$.

Problem 8

Let $k(q)=qe^{-q}$. Find the linear approximation for $k$ around $q=a$.

Problem 9

Let $m(y)=e^{y^2}$. Find the equation for the tangent line of the graph of $m$ at $y=b$.

Problem 10

Let $x(t) = t^3 \ln (t)$. What is the slope of the tangent line to the graph of $x$ at the point $t=2$. At the point $t=\bigstar$?

Problem 11

Let $y(z)=\ln(az)$ for some positive parameter $a$.

  1. What is $\diff{y}{z}$?
  2. What is $\diffn{y}{z}{2}$?

Problem 12

Let $z(y)=ce^{by}$ for some parameters $b$ and $c$.

  1. What is $z'(y)$?
  2. What is $z'(0)$?
  3. What is $z'(1/b)$?
  4. What is $z''(y)$?
  5. What is $z''(0)$?
  6. What is $z''(1/b)$?

Problem 13

Let $h(s)=(a^2+b^2)e^{s^2}$ for parameters $a$ and $b$.

  1. What is $h'(s)$?
  2. What is $h'(1)$?
  3. What is $h''(s)$?
  4. What is $h''(1)$?

Problem 14

Let $s(u)=\frac{1+u}{1-u}$. What is $s'(u)$?

Problem 15

Let $g(x)=x^2e^{-x}$. Find $g'(x)$.

Problem 16

Let $f(x)=x^ne^{-x}$, where $n$ is a parameter. Find $f'(x)$.

One you have worked on a few problems, you can compare your solutions to the ones we came up with.

Similar pages