A simple example of using the gradient theorem
If a vector field $\dlvf$ is a gradient field, meaning $\dlvf = \nabla f$ for some scalar-valued function $f$, then we can compute the line integral of $\dlvf$ along a curve $\dlc$ from some point $\vc{a}$ to some other point $\vc{b}$ as \begin{align*} \dlint = f(\vc{b}) - f(\vc{a}). \end{align*} This integral does not depend on the entire curve $\dlc$; it depends on only the endpoints $\vc{a}$ and $\vc{b}$. If we replaced $\dlc$ by another curve with the same endpoints, the integral would be unchanged. Hence $\dlvf$ is conservative (also called path-independent).
As an example, consider $f(x,y) = xy^2$, and let $\dlvf(x,y) = \nabla f(x,y) = (y^2, 2xy)$. Since we wrote $\dlvf$ as a gradient, we know that $\dlvf$ must be conservative.
What is $\dlint$ where $\dlc$ is the path $\dllp(t)=(t^2,2(t-2)^3)$ for $1 \le t \le 3$? The starting point is $\vc{a} = \dllp(1) = (1,-2)$, and the ending pont is $\vc{b} = \dllp(3) = (9,2)$. Hence the integral must be \begin{align*} \dlint &= f(9,2) - f(1,-2)\\ &= 9(2^2) - 1(-2)^2 = 36-4=32. \end{align*}
We could also compute $\dlint$ the direct way using the parametrization $\dllp(t)$. The integral isn't difficult as it is just a polynomial, but it is messy, so we'll skip the details. \begin{align*} \dlint &= \plint{a}{b}{\dlvf}{\dllp}\\ &= \int_1^3 \dlvf(t^2,2(t-2)^3) \cdot (2t, 6(t-2)^2) dt\\ &= \int_1^3 ((2(t-2)^3)^2 , 2t^22(t-2)^3)\cdot (2t,6(t-2)^2) dt\\ &=\int_1^3 8(t(t-2)^6+3t^2(t-2)^5)dt\\ &=8 (32 t^2 - 96 t^3 + 120 t^4 - 80 t^5 + 30 t^6 - 6 t^7 + t^8/2) \bigg|_1^3\\ &= 36-4 = 32, \end{align*} which agrees with the first answer.
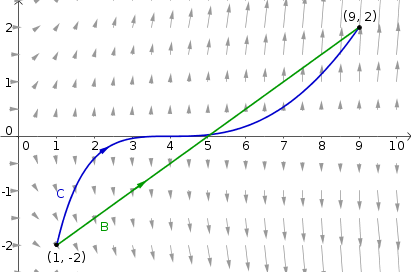
We should get the same answer for any path from $(1,-2)$ to $(9,2)$. Since $(9,2)-(1,-2) = (8,4)$, we let the curve $\adlc$ be the straight line path parametrized by $\adllp(t) = (1,-2) + t(8,4) = (1+8t, 4t-2)$ for $0 \le t \le 1$. This change is not a reparametrization of $\dlc$. The curve $\dlc$ was not a straight line, so $\adlc$ is a completely different curve, as you can see in the below figure, where $\dlc$ is shown in blue and $\adlc$ is shown in green.
The integral along $\adlc$ is \begin{align*} \lint{\adlc}{\dlvf} &= \plint{0}{1}{\dlvf}{\adllp}\\ &= \int_0^1 \dlvf(1+8t, 4t-2) \cdot (8,4) dt\\ &= \int_0^1 \left((4t-2)^2, 2(4t-2)(1+8t)\right) \cdot (8,4) dt\\ &= \int_0^1 (4-16t + 16t^2, -4 - 24 t + 64 t^2) \cdot (8,4) dt\\ &= \int_0^1 16(1 - 14 t + 24 t^2)dt\\ &= 16(t - 7 t^2 + 8 t^3)\bigg|_0^1 = 32. \end{align*} Indeed, we got the same answer again.
In this example, we were given the potential function at the outset, making the application of the gradient theorem particularly easy. If you aren't given the potential function, then to apply the gradient theorem, you'd need to test if the vector field is conservative and then find the potential function.
\end{document}Thread navigation
Multivariable calculus
- Previous: The gradient theorem for line integrals
- Next: How to determine if a vector field is conservative
Math 2374
Notation systems
Similar pages
- The gradient theorem for line integrals
- How to determine if a vector field is conservative
- A path-dependent vector field with zero curl
- A conservative vector field has no circulation
- Finding a potential function for conservative vector fields
- Finding a potential function for three-dimensional conservative vector fields
- Testing if three-dimensional vector fields are conservative
- An introduction to conservative vector fields
- The fundamental theorems of vector calculus
- More similar pages