Image: Change order of integration example region with sinusoid, x first
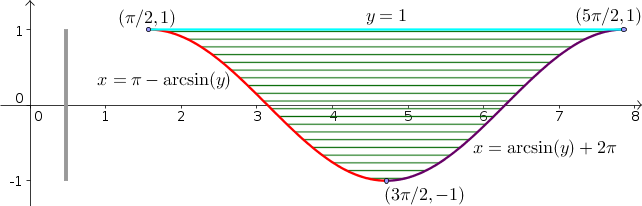Example region illustrating process of changing the order of integration in double integrals, shown with $x$ as the inner integral. For a given value of $y$, $x$ ranges from the curve $x=\pi - \arcsin y$ (red) to the curve $x=2\pi +\arcsin y$ (purple), as illustrated by the horizontal hashing over the region. The total range of $y$ over the region is from $-1$ to 1, as illustrated by the gray bar at the left.
Image file: double_integral_change_order_example_sin_x.png
Source image file: double_integral_change_order_example_sin_x.ggb
Source image type: Geogebra
Image links
This image is found in the pages