Examples of changing the order of integration in double integrals
Given a double integral \begin{align*} \iint_\dlr f(x,y)\,dA \end{align*} of a function $f(x,y)$ over a region $\dlr$, you may be able to write it as two different iterated integrals. You can integrate with respect to $x$ first, or you can integrate with respect to $y$ first. If you integrate with respect to $x$ first, you will obtain an integral that looks something like \begin{align*} \iint_\dlr f(x,y)\,dA = \int_{\Box}^{\Box} \left(\int_{\Box}^{\Box} f(x,y)\,dx \right) dy, \end{align*} and if you integrate with respect to $y$ first, you will obtain an integral that looks something like \begin{align*} \iint_\dlr f(x,y)\,dA = \int_{\Box}^{\Box} \left(\int_{\Box}^{\Box} f(x,y)\,dy \right) dx. \end{align*} We often say that the first integral is in $dx\,dy$ order and the second integral is in $dy\,dx$ order.
One difficult part of computing double integrals is determining the limits of integration, i.e., determining what to put in place of the boxes $\Box$ in the above integrals. In some situations, we know the limits of integration the $dx\,dy$ order and need to determine the limits of integration for the equivalent integral in $dy\,dx$ order (or vice versa). The process of switching between $dx\,dy$ order and $dy\,dx$ order in double integrals is called changing the order of integration (or reversing the order of integration).
Changing the order of integration is slightly tricky because its hard to write down a specific algorithm for the procedure. The easiest way to accomplish the task is through drawing a picture of the region $\dlr$. From the picture, you can determine the corners and edges of the region $\dlr$, which is what you need to write down the limits of integration.
We demonstrate this process with examples. The simplest region (other than a rectangle) for reversing the integration order is a triangle. You can see how to change the order of integration for a triangle by comparing example 2 with example 2' on the page of double integral examples. In this page, we give some further examples changing the integration order.
Example 1
Change the order of integration in the following integral \begin{align*} \int_0^1 \int_1^{e^y} f(x,y) dx\, dy. \end{align*} (Since the focus of this example is the limits of integration, we won't specify the function $f(x,y)$. The procedure doesn't depend on the identity of $f$.)
Solution: In the original integral, the integration order is $dx\,dy$. This integration order corresponds to integrating first with respect to $x$ (i.e., summing along rows in the picture below), and afterwards integrating with respect to $y$ (i.e., summing up the values for each row). Our task is to change the integration to be $dy\,dx$, which means integrating first with respect to $y$.
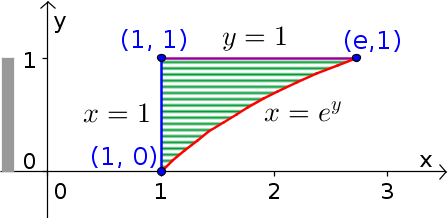
We begin by transforming the limits of integration into the domain $\dlr$. The limits of the outer $dy$ integral mean that $0 \le y \le 1,$ and the limits on the inner $dx$ integral mean that for each value of $y$ the range of $x$ is $1 \le x \le e^y.$ The region $\dlr$ is shown in the following figure.
The maximum range of $y$ over the region is from 0 to 1, as indicated by the gray bar to the left of the figure. The horizontal hashing within the figure indicates the range of $x$ for each value of $y$, beginning at the left edge $x=1$ (blue line) and ending at the right curve edge $x=e^y$ (red curve).
We have also labeled all the corners of the region. The upper-right corner is the intersection of the line $y=1$ with the curve $x=e^y$. Therefore, the value of $x$ at this corner must be $e=e^1=e$, and the point is $(e,1)$.
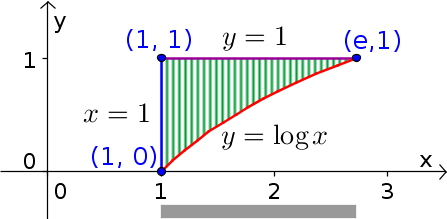
To change order of integration, we need to write an integral with order $dy\,dx$. This means that $x$ is the variable of the outer integral. Its limits must be constant and correspond to the total range of $x$ over the region $\dlr$. The total range of $x$ is $1 \le x \le e$, as indicated by the gray bar below the region in the following figure.
Since $y$ will be the variable for the inner integration, we need to integrate with respect to $y$ first. The vertical hashing indicates how, for each value of $x$, we will integrate from the lower boundary (red curve) to the upper boundary (purple line). These two boundaries determine the range of $y$. Since we can rewrite the equation $x=e^y$ for the red curve as $y=\log x$, the range of $y$ is $\log x \le y \le 1$. (The function $\log x$ indicates the natural logarithm, which sometimes we write as $\ln x$.)
In summary, the region $\dlr$ can be described not only by \begin{gather*} 0 \le y \le 1\\ 1 \le x \le e^y \end{gather*} as it was for the original $dx\,dy$ integral, but also by \begin{gather*} 1 \le x \le e\\ \log x \le y \le 1, \end{gather*} which is the description we need for the new $dy\,dx$ integration order. This latter pair of inequalites determine the bounds for integral.
We conclude that the integral$\int_0^1 \int_1^{e^y} f(x,y) dx\, dy$ with integration order reversed is \begin{align*} \int_1^e \int_{\log x}^1 f(x,y) dy \, dx. \end{align*}
Example 2
Sometimes you need to change the order of integration to get a tractable integral. For example, if you tried to evaluate \begin{align*} \int_0^1 \int_x^1 e^{y^2}dy\,dx \end{align*} directly, you would run into trouble. There is no antiderivative of $e^{y^2}$, so you get stuck trying to compute the integral with respect to $y$. But, if we change the order of integration, then we can integrate with respect to $x$ first, which is doable. And, it turns out that the integral with respect to $y$ also becomes possible after we finish integrating with respect to $x$.
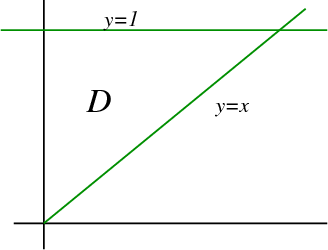
According to the limits of integration of the given integral, the region of integration is \begin{gather*} 0 \le x \le 1\\ x \le y \le 1, \end{gather*} which is shown in the following picture.
Since we can also describe the region by \begin{gather*} 0 \le y \le 1\\ 0 \le x \le y, \end{gather*} the integral with the order changed is \begin{align*} \int_0^1 \int_x^1 e^{y^2} dy\,dx = \int_0^1\int_0^y e^{y^2} dx\,dy \end{align*} With this new $dx\,dy$ order, we integrate first with respect to $x$ \begin{align*} \int_0^1\int_0^y e^{y^2} dx\,dy = \int_0^1 x \left.\left.e^{y^2}\right|_{x=0}^{x=y}\right. dy = \int_0^1 y e^{y^2} dy. \end{align*} Since the integration with respect to $x$ gave us an extra factor of $y$, we can compute the integral with respect to $y$ by using a $u$-substitution, $u=y^2$, so $du=2y\,dy$. With this substitution, $u$ rannges from 0 to 1, and we calculate the integral as \begin{align*} \int_0^1\int_0^y e^{y^2} dx\,dy &=\int_0^1 y e^{y^2} dy\\ &= \int_0^1 \frac{1}{2} e^{u} du = \frac{1}{2} e^{u} \bigg|_0^1 = \frac{1}{2}(e-1). \end{align*}
Example 3
Here's an example that's a bit more tricky. Reverse the order of integration in the following integral. \begin{gather*} \int_{\pi/2}^{5\pi/2} \int_{\sin x}^1 f(x,y) dy\,dx \end{gather*}
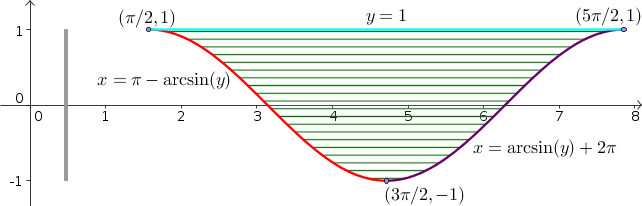
Solution: The region $\dlr$ described by this integral is \begin{gather*} \pi/2 \le x \le 5\pi/2\\ \sin x \le y \le 1. \end{gather*} as shown in the following image, where the total range on $x$ is shown by the gray bar below the region, and the variable boundaries for $y$ are shown by the blue and cyan curves.
One trick for changing variables with this region is correctly dealing with the lower boundary $y = \sin(x)$. When we solve this boundary equation for $x$ as a function of $y$, we may be tempted to write it as $x = \arcsin(y)$ and maybe even think that $x \le \arcsin(y)$ in the region.
Looking closely at the picture, we see this cannot be the case. In fact, the lower boundary for $y$ as a function of $x$ (the blue curve) has to be both the upper and lower boundaries for $x$ as a function of $y$, as shown by the red and purple curves in the below figure.
To get the formula for these boundaries, we have to remember how the inverse of the sinusoid, $\arcsin(y)$, is defined. In order to define the inverse of $\sin(x)$, we need to restrict the function to an interval where it takes on each value only one time. The standard way to define $\arcsin(y)$ is to restrict $\sin(x)$ to values of $x$ in the interval $[-\pi/2,\pi/2]$ as $\sin(x)$ ranges from $-1$ to 1 in that interval. This means that $\arcsin(y)$ ranges from $[-\pi/2,\pi/2]$ as $y$ goes from $-1$ to 1.
For the upper boundary of $x$ (in purple), $x$ ranges from $3\pi/2$ to $5\pi/2$. If we let $x=\arcsin(y)+2\pi$, then $x=3\pi/2$ when $y=-1$ and $x=5\pi/2$ when $y=1$, as required. For the lower boundary of $x$ (in red), we need $x$ to be a decreasing function of $y$, starting at $x=3\pi/2$ when $y=-1$ and decreasing to $x=\pi/2$ when $y=1$. These conditions are satisfied if we choose $x=\pi-\arcsin(y)$. If you are an expert at your trignometric identifies, you can verify that the equations for both of these curves are just different inverses of $\sin(x)$, as taking the sinusoid of these equations reduces them to $y=\sin(x)$.
Since in the region, $y$ ranges over the interval $[-1,1]$ (gray bar to the left of the region), we can describe the region $\dlr$ with the inequalities \begin{gather*} -1 \le y \le 1\\ \pi-\arcsin y \le x \le \arcsin y+2\pi. \end{gather*} This description of $\dlr$ is what we need to change the order of integration, and we find that \begin{gather*} \int_{\pi/2}^{5\pi/2} \int_{\sin x}^1 f(x,y) dy\,dx = \int_{-1}^{1} \int_{\pi-\arcsin y}^{\arcsin y+2\pi} f(x,y) dx\,dy. \end{gather*}
More examples
If you'd like more double integral examples, you can study some introductory double integral examples.. You can also take a look at double integral examples from the special cases of interpreting double integrals as area and double integrals as volume.
Thread navigation
Multivariable calculus
Math 2374
Similar pages
- Double integrals where one integration order is easier
- Introduction to double integrals
- Double integrals as iterated integrals
- Double integral examples
- Double integrals as volume
- Double integrals as area
- Triple integral examples
- Introduction to changing variables in double integrals
- Area calculation for changing variables in double integrals
- Double integral change of variable examples
- More similar pages