Image: A path-dependent vector field with zero curl
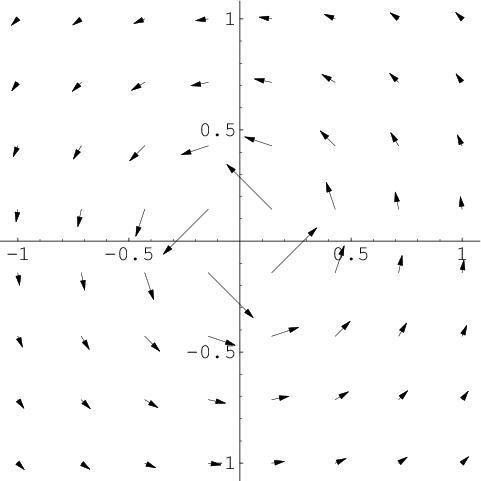The vector field
\begin{align*}
\dlvf(x,y) = \left( \frac{-y}{x^2+y^2}, \frac{x}{x^2+y^2} \right)
\end{align*}
has zero curl, as $\pdiff{\dlvfc_2}{x} - \pdiff{\dlvfc_1}{y}=0$. However, it is clearly path-dependent due to the counterclockwise circulation around the origin. Zero curl does not imply path-independence because the vector field is not defined at the origin, making its domain of definition be non-simply connected.
Image file: path_dependent_zero_curl.png
Image links
This image is found in the pages