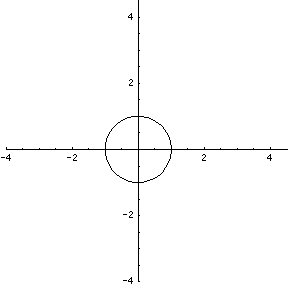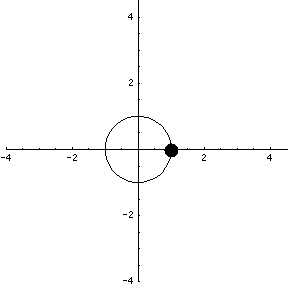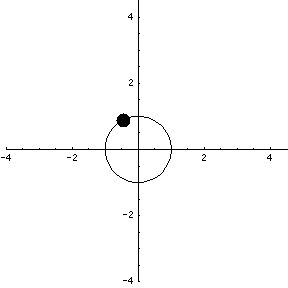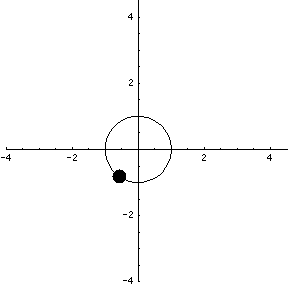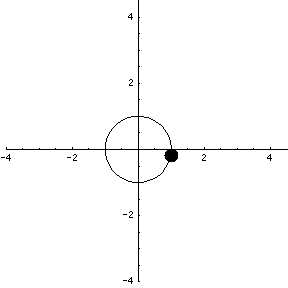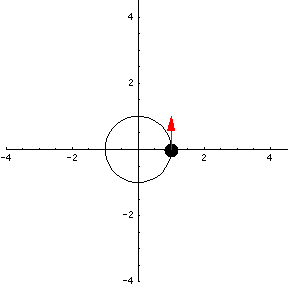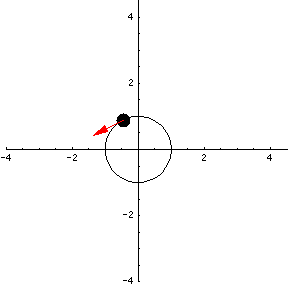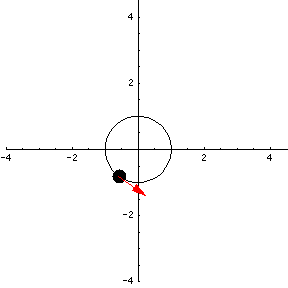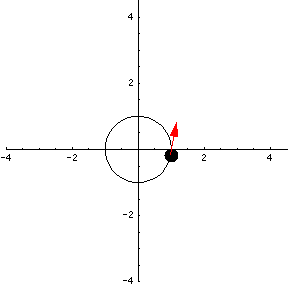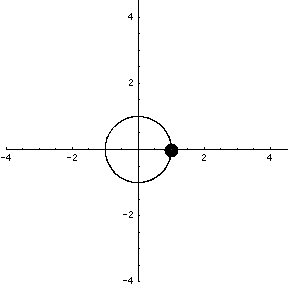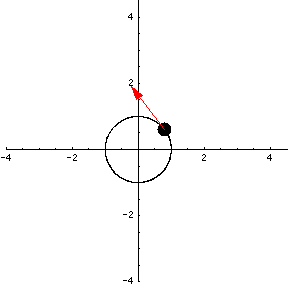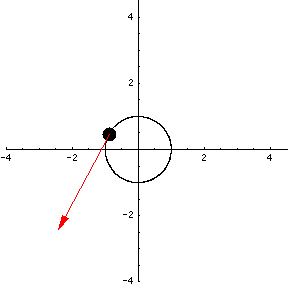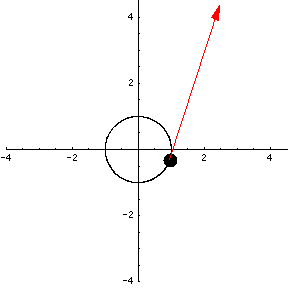Parametrized curve and derivative as location and velocity
A vector-valued function of a single variable $\dllp: \R \to \R^n$ (confused?) can be viewed as a parametrization of a curve, and its derivative is tangent to the curve. We can think of $t$ as time and the parametrization $\dllp(t)$ as being the position of an object at time $t$. The curve parametrized by $\dllp(t)$ is the trajectory of the particle.
For example, the function $\dllp(t) = (\cos t, \sin t)$ is a parametrization of the unit circle.
The parametrization, though, has more information that simply the circle. It gives the location of the particle moving around the circle, where the particle finishes each trip in $t=2\pi$ seconds (or minutes, or hours, or whatever units we use for time $t$). The following animation illustrates this motion.
It looks as if the speed of the particle is constant. We can show analytically that this is true. If $\dllp(t)$ represents the location of a particle at time $t$, the the velocity of the particle is $\dllp(t) = \dllp'(t)$, the derivative of $\dllp$. For our example, $\dllp(t) = (\cos t, \sin t)$, and the velocity is $\vc{v}(t) = \dllp'(t) = (-\sin t, \cos t)$.
Velocity is a little different than speed. Speed is just a number representing how fast a particle is moving. Velocity is a vector whose length represents speed, and whose direction represents the direction the particle is moving at that specific instance of time. We can add the velocity vector to our animation.
It certainly looks as if the length of the velocity vector is constant, which would confirm that the speed of the particle is constant. In fact, we can show this algebraically. You should find the length of the tangent vector $\vc{v}(t)$ on paper and show that it is constant -- it does not depend on t.
Let's look at a different parametrization of the unit circle, $\adllp(t) = (\cos(t^2), \sin(t^2))$, $0 \le t \le \sqrt{2\pi}.$
This is a parametrization of the unit circle because as $t$ ranges from $0$ to $\sqrt{2\pi}$, $t^2$ ranges from 0 to $2\pi$. Let's watch the particle whose motion is represented by $\adllp(t)$.
As you can see, the particle starts out very slowly and picks up speed as time goes on. You can see this either by watching the particle itself, or by watching the length of the tangent vector grow. (Remember, the length of the tangent vector represents the speed of the particle!) Find the velocity of this particle and see if you can explain what you're seeing.
Thread navigation
Multivariable calculus
Math 2374
Notation systems
Similar pages
- Derivatives of parameterized curves
- Tangent lines to parametrized curves
- An introduction to parametrized curves
- Tangent line to parametrized curve examples
- Line integrals are independent of parametrization
- Orienting curves
- Parametrization of a line
- Parametrization of a line examples
- Introduction to partial derivatives
- Partial derivative examples
- More similar pages