An introduction to vectors
Definition of a vector
A vector is an object that has both a magnitude and a direction. Geometrically, we can picture a vector as a directed line segment, whose length is the magnitude of the vector and with an arrow indicating the direction. The direction of the vector is from its tail to its head.
Two vectors are the same if they have the same magnitude and direction. This means that if we take a vector and translate it to a new position (without rotating it), then the vector we obtain at the end of this process is the same vector we had in the beginning.
Two examples of vectors are those that represent force and velocity. Both force and velocity are in a particular direction. The magnitude of the vector would indicate the strength of the force or the speed associated with the velocity.
We denote vectors using boldface as in $\vc{a}$ or $\vc{b}$. Especially when writing by hand where one cannot easily write in boldface, people will sometimes denote vectors using arrows as in $\vec{a}$ or $\vec{b}$, or they use other markings. We won't need to use arrows here. We denote the magnitude of the vector $\vc{a}$ by $\|\vc{a}\|$. When we want to refer to a number and stress that it is not a vector, we can call the number a scalar. We will denote scalars with italics, as in $a$ or $b$.
You can explore the concept of the magnitude and direction of a vector using the below applet. Note that moving the vector around doesn't change the vector, as the position of the vector doesn't affect the magnitude or the direction. But if you stretch or turn the vector by moving just its head or its tail, the magnitude or direction will change. (This applet also shows the coordinates of the vector, which you can read about in another page.)
The magnitude and direction of a vector. The blue arrow represents a vector $\vc{a}$. The two defining properties of a vector, magnitude and direction, are illustrated by a red bar and a green arrow, respectively. The length of the red bar is the magnitude $\|\vc{a}\|$ of the vector $\vc{a}$. The green arrow always has length one, but its direction is the direction of the vector $\vc{a}$. The one exception is when $\vc{a}$ is the zero vector (the only vector with zero magnitude), for which the direction is not defined. You can change either end of $\vc{a}$ by dragging it with your mouse. You can also move $\vc{a}$ by dragging the middle of the vector; however, changing the position of the $\vc{a}$ in this way does not change the vector, as its magnitude and direction remain unchanged.
There is one important exception to vectors having a direction. The zero vector, denoted by a boldface $\vc{0}$, is the vector of zero length. Since it has no length, it is not pointing in any particular direction. There is only one vector of zero length, so we can speak of the zero vector.
Operations on vectors
We can define a number of operations on vectors geometrically without reference to any coordinate system. Here we define addition, subtraction, and multiplication by a scalar. On separate pages, we discuss two different ways to multiply two vectors together: the dot product and the cross product.
Addition of vectors
Given two vectors $\vc{a}$ and $\vc{b}$, we form their sum $\vc{a}+\vc{b}$, as follows. We translate the vector $\vc{b}$ until its tail coincides with the head of $\vc{a}$. (Recall such translation does not change a vector.) Then, the directed line segment from the tail of $\vc{a}$ to the head of $\vc{b}$ is the vector $\vc{a}+\vc{b}$.
The vector addition is the way forces and velocities combine. For example, if a car is travelling due north at 20 miles per hour and a child in the back seat behind the driver throws an object at 20 miles per hour toward his sibling who is sitting due east of him, then the velocity of the object (relative to the ground!) will be in a north-easterly direction. The velocity vectors form a right triangle, where the total velocity is the hypotenuse. Therefore, the total speed of the object (i.e., the magnitude of the velocity vector) is $\sqrt{20^2+20^2}=20\sqrt{2}$ miles per hour relative to the ground.
Addition of vectors satisfies two important properties.
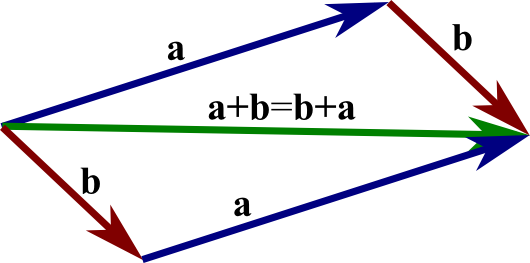
The commutative law, which states the order of addition doesn't matter: $$\vc{a}+\vc{b}=\vc{b}+\vc{a}.$$ This law is also called the parallelogram law, as illustrated in the below image. Two of the edges of the parallelogram define $\vc{a}+\vc{b}$, and the other pair of edges define $\vc{b}+\vc{a}$. But, both sums are equal to the same diagonal of the parallelogram.
The associative law, which states that the sum of three vectors does not depend on which pair of vectors is added first: $$(\vc{a}+\vc{b})+\vc{c} = \vc{a} + (\vc{b}+\vc{c}).$$
You can explore the properties of vector addition with the following applet. (This applet also shows the coordinates of the vectors, which you can read about in another page.)
The sum of two vectors. The sum $\vc{a}+\vc{b}$ of the vector $\vc{a}$ (blue arrow) and the vector $\vc{b}$ (red arrow) is shown by the green arrow. As vectors are independent of their starting position, both blue arrows represent the same vector $\vc{a}$ and both red arrows represent the same vector $\vc{b}$. The sum $\vc{a}+\vc{b}$ can be formed by placing the tail of the vector $\vc{b}$ at the head of the vector $\vc{a}$. Equivalently, it can be formed by placing the tail of the vector $\vc{a}$ at the head of the vector $\vc{b}$. Both constructions together form a parallelogram, with the sum $\vc{a}+\vc{b}$ being a diagonal. (For this reason, the commutative law $\vc{a}+\vc{b}=\vc{b}+\vc{a}$ is sometimes called the parallelogram law.) You can change $\vc{a}$ and $\vc{b}$ by dragging the yellow points.
Vector subtraction
Before we define subtraction, we define the vector $-\vc{a}$, which is the opposite of $\vc{a}$. The vector $-\vc{a}$ is the vector with the same magnitude as $\vc{a}$ but that is pointed in the opposite direction.
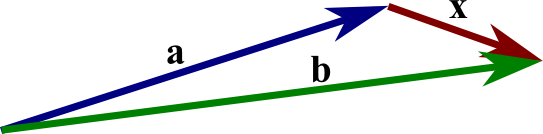
We define subtraction as addition with the opposite of a vector: $$\vc{b}-\vc{a} = \vc{b} + (-\vc{a}).$$ This is equivalent to turning vector $\vc{a}$ around in the applying the above rules for addition. Can you see how the vector $\vc{x}$ in the below figure is equal to $\vc{b}-\vc{a}$? Notice how this is the same as stating that $\vc{a}+\vc{x}=\vc{b}$, just like with subtraction of scalar numbers.
Scalar multiplication
Given a vector $\vc{a}$ and a real number (scalar) $\lambda$, we can form the vector $\lambda\vc{a}$ as follows. If $\lambda$ is positive, then $\lambda\vc{a}$ is the vector whose direction is the same as the direction of $\vc{a}$ and whose length is $\lambda$ times the length of $\vc{a}$. In this case, multiplication by $\lambda$ simply stretches (if $\lambda>1$) or compresses (if $0 < \lambda <1$) the vector $\vc{a}$.
If, on the other hand, $\lambda$ is negative, then we have to take the opposite of $\vc{a}$ before stretching or compressing it. In other words, the vector $\lambda\vc{a}$ points in the opposite direction of $\vc{a}$, and the length of $\lambda\vc{a}$ is $|\lambda|$ times the length of $\vc{a}$. No matter the sign of $\lambda$, we observe that the magnitude of $\lambda\vc{a}$ is $|\lambda|$ times the magnitude of $\vc{a}$: $\| \lambda \vc{a}\| = |\lambda| \|\vc{a}\|$.
Scalar multiplications satisfies many of the same properties as the usual multiplication.
- $s(\vc{a}+\vc{b}) = s\vc{a} + s\vc{b}$ (distributive law, form 1)
- $(s+t)\vc{a} = s\vc{a}+t\vc{a}$ (distributive law, form 2)
- $1\vc{a} = \vc{a}$
- $(-1)\vc{a} = -\vc{a}$
- $0\vc{a} = \vc{0}$
In the last formula, the zero on the left is the number 0, while the zero on the right is the vector $\vc{0}$, which is the unique vector whose length is zero.
If $\vc{a} = \lambda\vc{b}$ for some scalar $\lambda$, then we say that the vectors $\vc{a}$ and $\vc{b}$ are parallel. If $\lambda$ is negative, some people say that $\vc{a}$ and $\vc{b}$ are anti-parallel, but we will not use that language.
We were able to describe vectors, vector addition, vector subtraction, and scalar multiplication without reference to any coordinate system. The advantage of such purely geometric reasoning is that our results hold generally, independent of any coordinate system in which the vectors live. However, sometimes it is useful to express vectors in terms of coordinates, as discussed in a page about vectors in the standard Cartesian coordinate systems in the plane and in three-dimensional space.
Thread navigation
Vector algebra
Math 2374
Math 2241, Spring 2023
Similar pages
- Vectors in two- and three-dimensional Cartesian coordinates
- The cross product
- Cross product examples
- The formula for the cross product
- The scalar triple product
- Scalar triple product example
- Multiplying matrices and vectors
- Matrix and vector multiplication examples
- Vectors in arbitrary dimensions
- The transpose of a matrix
- More similar pages