The directional derivative
Let the function $f(x,y)$ be the height of a mountain range at each point $\vc{x} = (x,y)$. If you stand at some point $\vc{x}=\vc{a}$, the slope of the ground in front of you will depend on the direction you are facing. It might slope steeply up in one direction, be relatively flat in another direction, and slope steeply down in yet another direction.
The partial derivatives of $f$ will give the slope $\pdiff{f}{x}$ in the positive $x$ direction and the slope $\pdiff{f}{y}$ in the positive $y$ direction. We can generalize the partial derivatives to calculate the slope in any direction. The result is called the directional derivative.
The first step in taking a directional derivative, is to specify the direction. One way to specify a direction is with a vector $\vc{u}=(u_1,u_2)$ that points in the direction in which we want to compute the slope. For simplicity, we will insist that $\vc{u}$ is a unit vector. We write the directional derivative of $f$ in the direction $\vc{u}$ at the point $\vc{a}$ as $D_{\vc{u}}f(\vc{a})$. We could define it with a limit definition just as an ordinary derivative or a partial derivative \begin{align*} D_{\vc{u}}f(\vc{a}) = \lim_{h \to 0} \frac{f(\vc{a}+h\vc{u}) - f(\vc{a})}{h}. \end{align*} However, it turns out that for differentiable $f(x,y)$, we won't need to worry about that definition.
The concept of the directional derivative is simple; $D_{\vc{u}}f(\vc{a})$ is the slope of $f(x,y)$ when standing at the point $\vc{a}$ and facing the direction given by $\vc{u}$. If $x$ and $y$ were given in meters, then $D_{\vc{u}}\vc{f}(\vc{a})$ would be the change in height per meter as you moved in the direction given by $\vc{u}$ when you are at the point $\vc{a}$.
Note that $D_{\vc{u}}f(\vc{a})$ is a number, not a matrix. In fact, the directional derivative is the same as a partial derivative if $\vc{u}$ points in the positive $x$ or positive $y$ direction. For example, if $\vc{u}=(1,0)$, then $\displaystyle D_{\vc{u}}f(\vc{a}) = \pdiff{f}{x}(\vc{a})$. Similarly if $\vc{u}=(0,1)$, then $\displaystyle D_{\vc{u}}f(\vc{a}) = \pdiff{f}{y}(\vc{a})$.
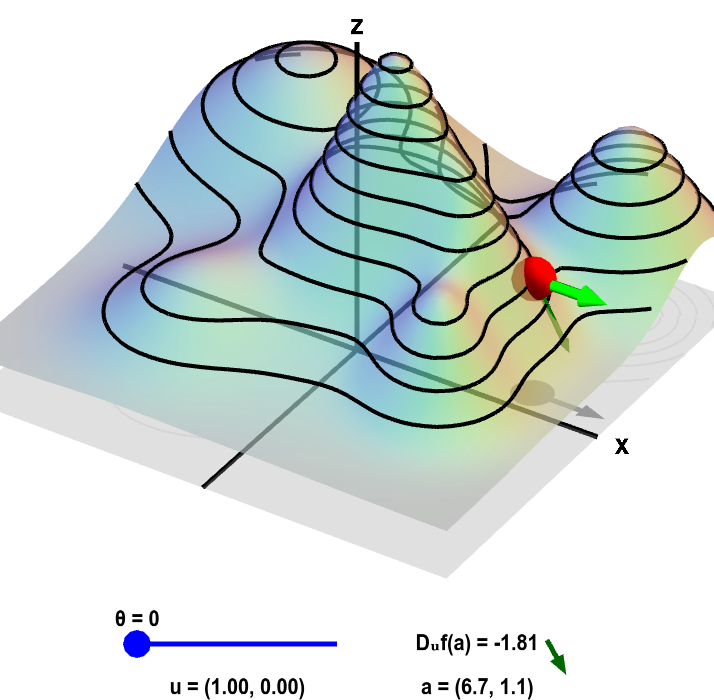
In the following applet, the height $f(x,y)$ of a mountain range is shown as a level curve plot. You can recognize two steep mountain peaks by the closely spaced circular level curves. In this applet, you can move the point $\vc{a}$ around, change the direction $\vc{u}$ and observe how the directional derivative $D_{\vc{u}}f(\vc{a})$ changes. If you set $\vc{u}$ to point straight east ($\theta=0$ in the applet), then $\vc{u}$ points in the positive $x$ direction ($\vc{u}=(1,0)$) so that $\displaystyle D_{\vc{u}}f(\vc{a}) = \pdiff{f}{x}(\vc{a})$. Similarly, when $\vc{u}$ points straight north ($\theta=\pi/2$), then $\vc{u}$ points in the positive $y$ direction ($\vc{u}=(0,1)$) so that $\displaystyle D_{\vc{u}}f(\vc{a}) = \pdiff{f}{y}(\vc{a})$.
Directional derivative on a mountain shown as level curves. The height of a mountain ranged described by a function $f(x,y)$ is shown as a level curve plot. A point $\vc{a}$ (in dark red) can be moved with the mouse. The height $f(\vc{a})$ is shown on the bottom cyan slider labeled by “f”. The direction vector $\vc{u}$ (the light green vector) points at an angle $\theta$ from east, which can be changed by dragging the red point on the top slider. The value of the directional derivative $D_{\vc{u}}f(\vc{a})$ is shown by the middle (light green) slider labeled by “Duf”.
If you make $\vc{u}$ point in a direction parallel to the level curve, what happens to $D_{\vc{u}} f(\vc{a})$? (Since the height is constant along a level curve, you should be able to infer what the slope in that direction should be.) What happens to $D_{\vc{u}}f(\vc{a})$ when you turn $\vc{u}$ to point in the opposite direction (i.e., add or subtract $\pi$ from $\theta$)?
To help you visualize what is going on in case you are not yet comfortable with level curve plots, a second applet, below, duplicates the above applet but with a mesh plot of the surface $z=f(x,y)$. In this view, the steepness may be easier to see. However, this view is a little misleading for two reasons. First, the dark red dot now floats on the surface of the mountain. Hence, the dark red dot is no longer $\vc{a}$, which for this example is really a point in two dimensions. Second, the light green vector is now a three-dimensional vector that points up or down the mountain. The light green vector is no longer exactly the direction vector $\vc{u}$, which for this example is really a two-dimensional vector. Nonetheless, this second view further illustrates the concepts of the directional derivative. You can use it to help you understand what is happening in the above level curve plot.
Directional derivative on a mountain shown as mesh plot. The height of a mountain ranged described by a function $f(x,y)$ is shown as a mesh plot. A point $\vc{b}$ (in dark red) can be moved with the mouse. The vector $\vc{v}$ (the light green vector) points at an angle $\theta$ from east, which can be changed by dragging the red point on the top slider. Although $\vc{b}$ and $\vc{v}$ are in three dimensions, we can imagine projecting them to the $xy$-plane, giving the point $\vc{a}$ and unit vector $\vc{u}$. The value of the directional derivative $D_{\vc{u}}f(\vc{a})$ is shown by the bottom (light green) slider labeled by “Duf”.
The gradient
In most cases, there is always one direction $\vc{u}$ where the directional derivative $D_{\vc{u}}f(\vc{a})$ is the largest. This is the “uphill” direction. (In some cases, such as when you are at the top of a mountain peak or at the lowest point in a valley, this might not be true.) Let's call this direction of maximal slope $\vc{m}$. Both the direction $\vc{m}$ and the maximal directional derivative $D_{\vc{m}}f(\vc{a})$ are captured by something called the gradient of $f$ and denoted by $\nabla f(\vc{a})$. The gradient is a vector that points in the direction of $\vc{m}$ and whose magnitude is $D_{\vc{m}}f(\vc{a})$. In math, we can write this as $\displaystyle \frac{\nabla f(\vc{a})}{\| \nabla f(\vc{a})\|} = \vc{m}$ and $\| \nabla f(\vc{a})\| = D_{\vc{m}}f(\vc{a})$.
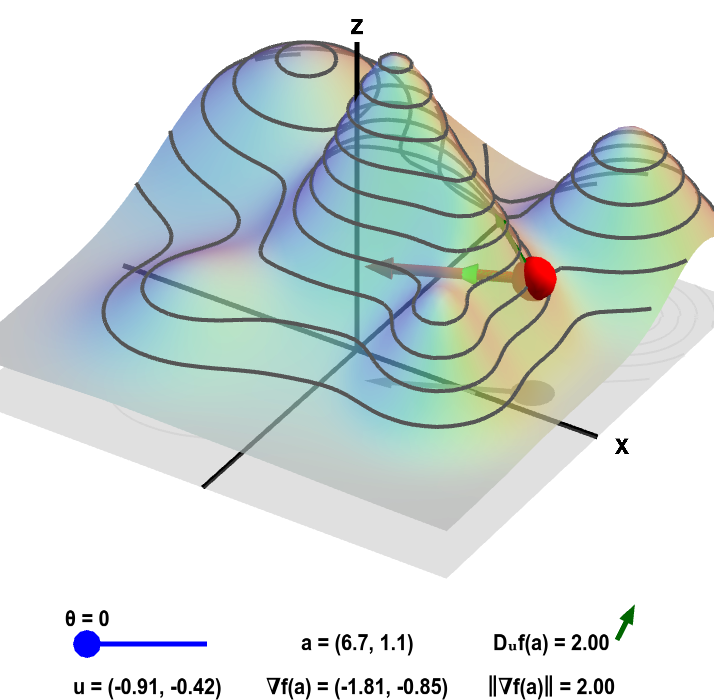
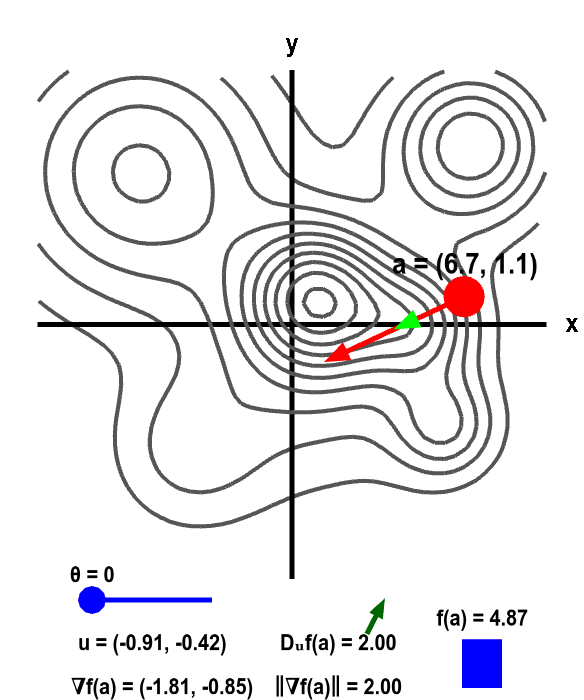
The below applet illustrates the gradient, as well as its relationship to the directional derivative. The definition of $\theta$ is different from that of the above applets. Here $\theta$ is the angle between the gradient and vector $\vc{u}$. When $\theta=0$, $\vc{u}$ points in the same direction as the gradient (and is hidden in the applet).
Gradient and directional derivative on a mountain shown as level curves. The height of a mountain ranged described by a function $f(x,y)$ is shown as a level curve plot. A point $\vc{a}$ (in dark red) can be moved with the mouse. The height $f(\vc{a})$ is shown on the bottom cyan slider labeled by “f”. The direction of steepest increase of $f$ is given by the gradient vector $\nabla f(\vc{a})$ (the dark blue vector is ten times longer than the actual gradient). The actual length of the gradient $\| \nabla f(\vc{a})\|$ is shown by the dark blue line on the middle (light green) slider. The light green line on that slider indicates the value of the directional derivative $D_{\vc{u}}f(\vc{a})$, where $\vc{u}$ is represented by the light green vector coming out of $\vc{a}$. The direction of $\vc{u}$ is controlled by $\theta$ (changed via top slider), where $\theta$ is the angle between $\nabla f(\vc{a})$ and $\vc{u}$.
Notice how the dark blue gradient vector always points up the mountains (in fact, the gradient is always perpendicular to the level curves). When the level curves are close together, the gradient is large. What happens to the gradient at the tops of the mountains?
Note that when $\theta=0$ (or $\theta = 2\pi$), the directional derivative $D_{\vc{u}}f(\vc{a})$ (shown by the light green line on the middle slider) and the magnitude of the gradient $\|\nabla f (\vc{a})\|$ (shown by the dark blue line on the middle slider) are identical, i.e., $D_{\vc{u}}f(\vc{a}) = \| \nabla f(\vc{a})\|$. When $\theta=\pi$, then $\vc{u}$ points in the opposite direction of the gradient, and $D_{\vc{u}}f(\vc{a}) = - \| \nabla f(\vc{a})\|$. For what values of $\theta$ is $D_{\vc{u}}f(\vc{a}) = 0$?
By moving $\vc{a}$ (the dark red point) around and changing $\theta$, I hope you can convince yourself that, for a fixed $\vc{a}$, the maximal value of $D_{\vc{u}}f(\vc{a})$ occurs when $\vc{u}$ and $\nabla f (\vc{a})$ point in the same direction (i.e., when $\theta=0$ or $\theta=2\pi$), and the minimum value occurs when $\vc{u}$ and $\nabla f (\vc{a})$ point in opposite directions (i.e., when $\theta=\pi$). Hence $D_{\vc{u}}f(\vc{a})$ always lies between $-\| \nabla f(\vc{a})\|$ and $\| \nabla f(\vc{a})\|$. It turns out that the relationship between the gradient and the directional derivative can be summarized by the equation \begin{align*} D_{\vc{u}}f(\vc{a}) &= \nabla f(\vc{a}) \cdot \vc{u}\\ &= \|\nabla f(\vc{a})\|\, \| \vc{u}\| \cos\theta\\ &= \| \nabla f(\vc{a})\| \cos\theta \end{align*} where $\theta$ is the angle between $\vc{u}$ and the gradient. (Recall that $\vc{u}$ is a unit vector, meaning that $\| \vc{u}\|=1$.)
The applet is repeated using a plot of $z=f(x,y)$, below. Although its steepness may be easier to see, recall from the above discussion that the dark red point is no longer really $\vc{a}$ and the light green vector is no longer really $\vc{u}$. Similarly, since the dark blue vector points up the mountain, it is no longer really the gradient $\nabla f(\vc{a})$, which, for a function $f(x,y)$ of two variables, is a two-dimensional vector. Despite its shortcomings, this applet may help you see how the gradient always points in the direction where the mountain rises most steeply.
Gradient and directional derivative on a mountain shown as mesh plot. The dark red point can be moved along the mountain range whose height is given by $f(x,y)$. The dark blue vector points in the direction of the gradient. The magnitude of the gradient is shown by the dark blue line on the light green slider. The light green vector points at an angle $\theta$ (changeable via the top slider) from the gradient; the directional derivative in that direction is shown by the light green line on the light green slider. The dark blue and the light green vectors are shown as three-dimensional vectors titling up or down the mountain, and hence are not exactly the two dimensional vectors $\nabla f$ or the $\vc{u}$ of $D_{\vc{u}}f$.
But what exactly is the gradient?
This page was designed to give you an intuitive feel for what the directional directive and gradient are. But, we've failed to mention what exactly is the gradient. The above formula for the directional derivative is nice, but it's not very useful if you don't know how to calculate $\nabla f$. Fortunately, the end result is fairly simple, as the gradient is just a reformulation of the matrix of partial derivatives. You can check out a simple derivation of the gradient to see why this is true.
Once you know how to calculate the gradient, you can follow these examples.