The hyperboloid of one sheet
The hyperboloid of one sheet
Equation: $\displaystyle\frac{x^2}{A^2}+\frac{y^2}{B^2} - \frac{z^2}{C^2} = 1$
The hyperboloid of one sheet is possibly the most complicated of all the quadric surfaces. For one thing, its equation is very similar to that of a hyperboloid of two sheets, which is confusing. (See the page on the two-sheeted hyperboloid for some tips on telling them apart.) For another, its cross sections are quite complex.
Having said all that, this is a shape familiar to any fan of the Simpsons, or even anybody who has only seen the beginning of the show. A hyperboloid of one sheet looks an awful lot like a cooling tower at the Springfield Nuclear Power Plant.
Below, you can see the cross sections of a simple one-sheeted hyperboloid with $A=B=C=1$. The horizontal cross sections are ellipses -- circles, even, in this case -- while the vertical cross sections are hyperbolas. The reason I said they are so complex is that these hyperbolas can open up and down or sideways, depending on what values you choose for $x$ and $y$. Check the example and see for yourself. Yikes! If you do these cross sections by hand, you have to check an awful lot of special cases.
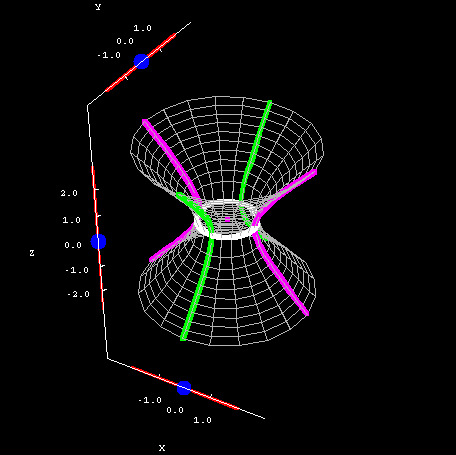
Hyperboloid of one sheet cross sections. The hyperboloid of one sheet $x^2+y^2-z^2=1$ is plotted along with its cross sections. You can drag the blue points on the sliders to change the location of the different types of cross sections.
The constants $A$, $B$, and $C$ once again affect how much the hyperboloid stretches in the x-, y-, and z-directions. You can see this for yourself in the second applet. Notice how quickly the hyperboloid grows, particularly in the $z$-direction. When $C=2$, a relatively small number, the surface already stretches from -8 to +8 on the $z$-axis.
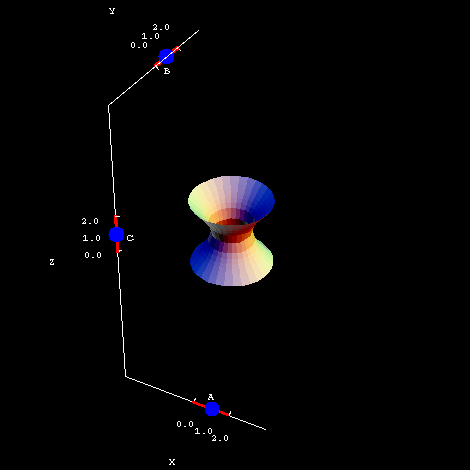
Hyperboloid of one sheet coefficients. The hyperboloid of one sheet $\frac{x^2}{A^2}+\frac{y^2}{B^2} - \frac{z^2}{C^2} = 1$ is plotted. You can drag the blue points on the sliders to change the coefficients $A$, $B$, and $C$.
One caveat: the applet only shows a small portion of the hyperboloid, but it continues on forever. So adjusting the value of $C$ doesn't really make the surface taller -- it's already "infinitely" tall -- but it certainly does affect the shape and slope of the surface. If you know something about partial derivatives, you could investigate how quickly $z$ changes with respect to $x$ and $y$ for different values of $C$. You could also explore why adjusting $C$ seems to have a more dramatic effect than changing $A$ and $B$.
Here are a few more points for you to consider.
- Once again, the sliders don't go all the way to 0. Why not? Make all of them as small as possible and zoom in to see the resulting hyperboloid.
- Look at the equation. What should happen when $x=A$ or $x=-A$? Check this in the first applet; recall that $A=1$ there.
- Does there always have to be a “hole” through the hyperboloid, or could the sides touch at the origin? In other words, could the cross section given by $z=0$ ever be a point instead of an ellipse? Experiment with the second applet; be sure to look directly from the top and zoom in before just assuming that the hole is gone.
List of quadric surfaces
- Elliptic paraboloid
- Hyperbolic paraboloid
- Ellipsoid
- Double cone
- Hyperboloid of one sheet
- Hyperboloid of two sheets
Thread navigation
Interactive Gallery of Quadric Surfaces
- Previous: The double cone
- Next: The hyperboloid of two sheets