Introduction to Taylor's theorem for multivariable functions
Remember one-variable calculus Taylor's theorem. Given a one variable function $f(x)$, you can fit it with a polynomial around $x=a$.
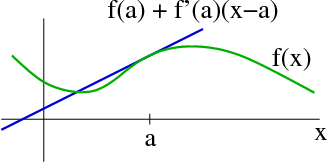
For example, the best linear approximation for $f(x)$ is \begin{align*} f(x) \approx f(a) + f\,'(a)(x-a). \end{align*} This linear approximation fits $f(x)$ (shown in green below) with a line (shown in blue) through $x=a$ that matches the slope of $f$ at $a$.
We can add additional, higher-order terms, to approximate $f(x)$ better near $a$. The best quadratic approximation is \begin{align*} f(x) \approx f(a) + f\,'(a)(x-a) + \frac{1}{2} f\,''(a)(x-a)^2 \end{align*} We could add third-order or even higher-order terms: \begin{align*} f(x) \approx f(a) + f\,'(a)(x-a) + \frac{1}{2} f\,''(a)(x-a)^2 + \frac{1}{6} f\,'''(a)(x-a)^3 + \cdots. \end{align*} The important point is that this Taylor polynomial approximates $f(x)$ well for $x$ near $a$.
We want to generalize the Taylor polynomial to (scalar-valued) functions of multiple variables: \begin{align*} f(\vc{x})= f(x_1,x_2, \ldots, x_n). \end{align*}
We already know the best linear approximation to $f$. It involves the derivative, \begin{align*} f(\vc{x}) \approx f(\vc{a}) + Df(\vc{a}) (\vc{x}-\vc{a}). \label{eq:firstorder} \end{align*} where $Df(\vc{a})$ is the matrix of partial derivatives. The linear approximation is the first-order Taylor polynomial.
What about the second-order Taylor polynomial? To find a quadratic approximation, we need to add quadratic terms to our linear approximation. For a function of one-variable $f(x)$, the quadratic term was \begin{align*} \frac{1}{2} f\,''(a)(x-a)^2. \end{align*} For a function of multiple variables $f(\vc{x})$, what is analogous to the second derivative?
Since $f(\vc{x})$ is scalar, the first derivative is $Df(\vc{x})$, a $1 \times n$ matrix, which we can view as an $n$-dimensional vector-valued function of the $n$-dimensional vector $\vc{x}$. For the second derivative of $f(\vc{x})$, we can take the matrix of partial derivatives of the function $Df(\vc{x})$. We could write it as $DDf(\vc{x})$ for the moment. This second derivative matrix is an $n \times n$ matrix called the Hessian matrix of $f$. We'll denote it by $Hf(\vc{x})$, \begin{align*} Hf(\vc{x}) = DDf(\vc{x}). \end{align*}
When $f$ is a function of multiple variables, the second derivative term in the Taylor series will use the Hessian $Hf(\vc{a})$. For the single-variable case, we could rewrite the quadratic expression as \begin{align*} \frac{1}{2} (x-a)f\,''(a)(x-a). \end{align*} The analog of this expression for the multivariable case is \begin{align*} \frac{1}{2} (\vc{x}-\vc{a})^T Hf(\vc{a}) (\vc{x}-\vc{a}). \end{align*}
We can add the above expression to our first-order Taylor polynomial to obtain the second-order Taylor polynomial for functions of multiple variables: \begin{align*} f(\vc{x}) \approx f(\vc{a}) + Df(\vc{a}) (\vc{x}-\vc{a}) + \frac{1}{2} (\vc{x}-\vc{a})^T Hf(\vc{a}) (\vc{x}-\vc{a}). \end{align*} The second-order Taylor polynomial is a better approximation of $f(\vc{x})$ near $\vc{x}=\vc{a}$ than is the linear approximation (which is the same as the first-order Taylor polynomial). We'll be able to use it for things such as finding a local minimum or local maximum of the function $f(\vc{x})$.
You can read some examples here.
Thread navigation
Multivariable calculus
- Previous: Directional derivative and gradient examples
- Next: Multivariable Taylor polynomial example
Math 2374
- Previous: Divergence theorem examples
- Next: Multivariable Taylor polynomial example
Similar pages
- Multivariable Taylor polynomial example
- Introduction to partial derivatives
- Partial derivative examples
- Partial derivative by limit definition
- Introduction to differentiability in higher dimensions
- The multivariable linear approximation
- Examples of calculating the derivative
- The definition of differentiability in higher dimensions
- Subtleties of differentiability in higher dimensions
- The derivative matrix
- More similar pages