The definition of differentiability in higher dimensions
The definition of differentiability in multivariable calculus formalizes what we meant in the introductory page when we referred to differentiability as the existence of a linear approximation. The introductory page simply used the vague wording that a linear approximation must be a “really good” approximation to the function near a point. What does this “really good” mean?
For a scalar valued function of two variables, $f: \R^2 \to \R$ (confused?), this condition meant the existence of a tangent plane, such as the one shown in this applet, which is the example used in the introductory page.
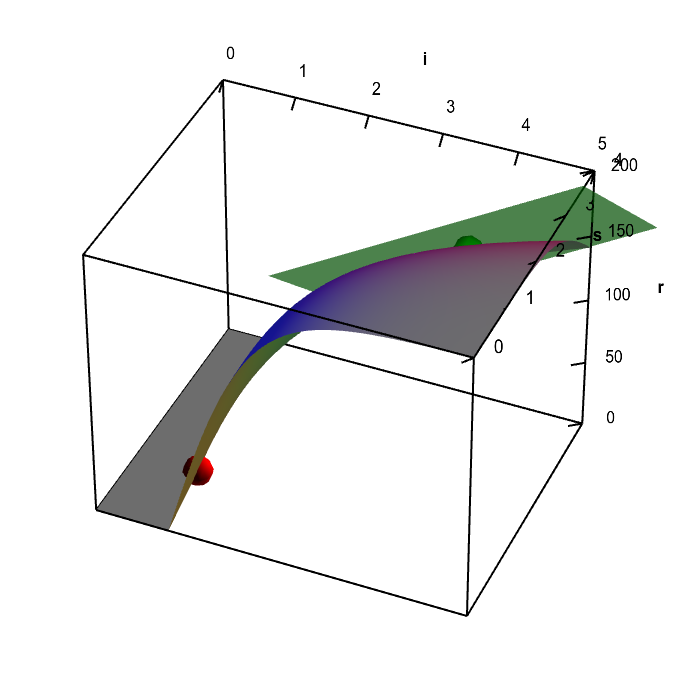
Applet loading
Neuron firing rate function with tangent plane. A fictitious representation of the firing rate $r(i,s)$ of a neuron in response to an input $i$ and nicotine level $s$. The graph of the function has a tangent plane at the location of the green point, so the function is differentiable there. By rotating the graph, you can see how the tangent plane touches the surface at the that point. You can move the green point anywhere on the surface; as long as it is not along the fold of the graph (where the red point in constrained to be), you can see the tangent plane showing that the function is differentiable. There is no tangent plane to the graph at any point along the fold of the graph (you can move the red point to any point along this fold). The function $r(i,s)$ is not differentiable at any point along the fold. As further evidence of this non-differentiability, the tangent plane jumps to a different angle when you move the green point across the fold.
Although we have geometric intuition that helps us understand a tangent plane, this intuition doesn't help us understand the general case of a linear approximation of a function $\vc{f}: \R^n \to \R^m$. Even for the two-dimensional case where differentiability is based on existence of a tangent plane, we should still be precise about what me mean by the existence of this linear approximation. Otherwise, we could never be certain if a given plane was really tangent to the graph.
How can we formalize this definition? For starters, let's write our candidate linear approximation around the point $\vc{a}$ as \begin{align*} \vc{L}(\vc{x}) = \vc{f}(\vc{a}) + \vc{T}(\vc{x}-\vc{a}) \end{align*} where $\vc{T}(\vc{x})$ is a linear transformation. We want to derive a condition to test if $\vc{L}$ really is the linear approximation of $\vc{f}$ around $\vc{a}$. The condition needs to capture the sense that $\vc{L}(\vc{x})$ is “really close” to $\vc{f}(\vc{x})$ when $\vc{x}$ is near $\vc{a}$.
One possibility might be that the limit of $\vc{L}(\vc{x})$ as $\vc{x}$ approaches $\vc{a}$ should be the same as the limit of $\vc{f}(\vc{x})$ as $\vc{x}$ approaches $\vc{a}$. That sounds reasonable. That would mean that distance between $\vc{L}(\vc{x})$ and $\vc{f}(\vc{x})$ should go to zero as we get close to $\vc{a}$. We could write this candidate condition as $$\lim_{\vc{x} \to \vc{a}} \| \vc{f}(\vc{x})-\vc{L}(\vc{x})\| = 0.$$ You can't get any closer than zero distance, so certainly this condition should be a good one.
The problem with this definition becomes immediately clear if you try to apply it to the one variable linear approximation, i.e., the tangent line of a curve. As shown in the following figure, many lines satisfy the above condition, as it only specifies that the line passes through the point $(a,f(a))$. Since the lines and the function are continuous, their distance clearly goes to zero as $x$ approaches $a$. How can we pick out the tangent line (shown in blue) to the graph of $f(x)$ (shown in green) from among all these candidate lines?
In hindsight, we can see that our above condition was doomed to failure. Reviewing the definition of a linear transformation reminds us that for any linear transformation $\vc{T}(\vc{x})$, it must be true that $\vc{T}(\vc{0})=\vc{0}$. So, given the above definition of $\vc{L}(\vc{x})$, we can see that $\vc{L}(\vc{a}) = \vc{f}(\vc{a})$ no matter what we choose for $\vc{T}(\vc{x})$. The condition $$\lim_{\vc{x} \to \vc{a}} \| \vc{f}(\vc{x})-\vc{L}(\vc{x})\| = 0$$ doesn't restrict the choice of $\vc{T}(\vc{x})$ at all.
We need a new, stronger condition that enforces that not only does $\| \vc{f}(\vc{x})-\vc{L}(\vc{x})\|$ go to zero as $\vc{x} \to \vc{a}$, but that it goes to zero fast.
To derive this condition, let's go back to single variable functions $f(x)$. In fact, let's simplify to the case where $f(x)$ is a quadratic function, which, without loss of generality, we can write as $$f(x) = A + B(x-a) + C(x-a)^2,$$ where $A$, $B$, and $C$ are just real constants. A linear transformation in one variable must be of the form $T(x)=mx$, so our candidate linear approximation can be written $$L(x) = f(a)+T(x-a) = A+m(x-a).$$ The difference between $f$ and $L$ is $$|f(x)-L(x)| = |B(x-a)+C(x-a)^2-m(x-a)|.$$ We want a condition that this expression must go to zero very fast as $x \to a$, and the condition must be strong enough to uniquely determine $m$.
Since all the terms in $|f(x)-L(x)|$ include a factor $(x-a)$, we know that it must go to zero at least as fast as $|x-a|$. If we want to impose a stronger condition, we must insist that it go to zero faster than $|x-a|$. How do we impose such a condition? We could divide by $|x-a|$ and insist that the result still goes to zero as $x \to a$. Then our candidate condition would be $$\lim_{x \to a} \frac{|f(x)-L(x)|}{|x-a|} = 0.$$
Does this work? Plug in our example quadratic function, and the condition becomes $$\lim_{x \to a} \frac{|B(x-a)+C(x-a)^2-m(x-a)|}{|x-a|} = 0$$ which simplifies to $$\lim_{x \to a} |B+C(x-a)-m| = 0.$$ Since $C(x-a) \to 0$ as $x \to a$, we see that our condition does indeed put a nice constraint on our linear transformation $T(x)=mx$. We are forced to conclude that $L(x)$ is a linear approximation of $f$ at $x=a$ only if $m=B$. This worked perfectly. Given that $B=f'(a)$, we see that this condition gives that the slope of the linear approximation (or tangent line) $L(x)$ is the derivative, consistent with what we learned in single-variable calculus.
Motivated by our single variable example, we propose the following condition for differentiability in general: $$\lim_{\vc{x} \to \vc{a}} \frac{\| \vc{f}(\vc{x})-\vc{L}(\vc{x})\|}{\|\vc{x}-\vc{a}\|} = 0.$$ This condition means that $\| \vc{f}(\vc{x})-\vc{L}(\vc{x})\|$ goes to zero very fast as $\vc{x} \to \vc{a}$, faster than the distance $\|\vc{x}-\vc{a}\|$ between $\vc{x}$ and $\vc{a}$ goes to zero. This condition is what we meant in the introduction to differentiability when we said that the linear approximation $\vc{L}(\vc{x})$ must be a “really good” approximation to $\vc{f}(\vc{x})$ when $\vc{x}$ is close to $\vc{a}$.
Definition of differentiability
We summarize our results with the definition differentiability. For simplicity, we'll write the definition directly in terms of the linear transformation $\vc{T}(x)$ without explicitly referring to the linear approximation $\vc{L}(\vc{x})$.
Definition: The function $\vc{f}: \R^n \to \R^m$ is differentiable at the point $\vc{a}$ if there exists a linear transformation $\vc{T}: \R^n \to \R^m$ that satisfies the condition $$\lim_{\vc{x} \to \vc{a}} \frac{\| \vc{f}(\vc{x})-\vc{f}(\vc{a}) - \vc{T}(\vc{x}-\vc{a})\|}{\|\vc{x}-\vc{a}\|} = 0.$$
The $m \times n$ matrix associated with the linear transformation $\vc{T}$ is the matrix of partial derivatives, which we denote by $\jacm{f}(\vc{a})$. We can refer to $\jacm{f}(\vc{a})$ as the total derivative (or simply the derivative) of $\vc{f}$.
What does that limit really mean?
It was a lot of work to derive a sensible expression for the definition of differentiability. You deserve to rest after getting through this. But don't rest for long because there are some more important subtleties lurking in that limit definition. It turns out that a limit in two or more dimensions is a bit more complicated than a limit in one dimension. One has to worry about the many different ways in which you can approach the point $\vc{a}$. In one dimension, you can only approach from either above or below, but more dimensions gives you a lot more room to move around.
For a function to be differentiable, we need the limit defining the differentiability condition to be satisfied, no matter how you approach the limit $\vc{x} \to \vc{a}$. This requirement can lead to some surprises, so you have to be careful. For example, don't make the mistake of assuming that the existence of partial derivatives is enough to ensure differentiability. You've been warned! Maybe it'd be best to check out the subtleties of differentiability in higher dimension so you'll be prepared for any function you might meet.
Thread navigation
Multivariable calculus
- Previous: Introduction to differentiability in higher dimensions
- Next: Subtleties of differentiability in higher dimensions
Math 2374
Similar pages
- Introduction to differentiability in higher dimensions
- Examples of calculating the derivative
- Subtleties of differentiability in higher dimensions
- The derivative matrix
- The multivariable linear approximation
- An introduction to the directional derivative and the gradient
- Derivation of the directional derivative and the gradient
- Introduction to Taylor's theorem for multivariable functions
- The multidimensional differentiability theorem
- Non-differentiable functions must have discontinuous partial derivatives
- More similar pages
