Distance from point to plane
Here's a quick sketch of how to calculate the distance from a point $P=(x_1,y_1,z_1)$ to a plane determined by normal vector $\vc{N}=(A,B,C)$ and point $Q=(x_0,y_0,z_0)$. The equation for the plane determined by $\vc{N}$ and $Q$ is $A(x-x_0)+B(y-y_0) +C(z-z_0) = 0$, which we could write as $Ax+By+Cz+D=0$, where $D=-Ax_0-By_0-Cz_0$.
This applet demonstrates the setup of the problem and the method we will use to derive a formula for the distance from the plane to the point $P$.
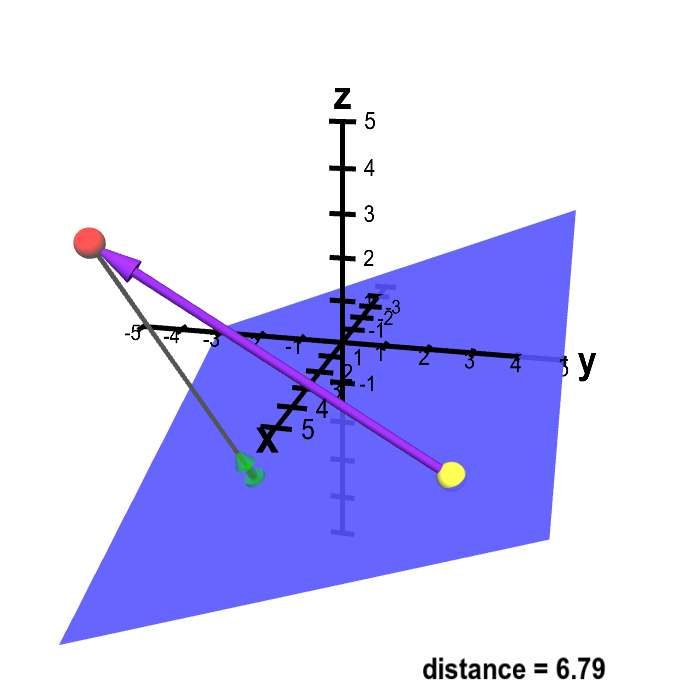
Applet loading
Distance from point to plane. A sketch of a way to calculate the distance from point $\color{red}{P}$ (in red) to the plane. The vector $\color{green}{\vc{n}}$ (in green) is a unit normal vector to the plane. You can drag point $\color{red}{P}$ as well as a second point $\vc{Q}$ (in yellow) which is confined to be in the plane. Although the vector $\color{green}{\vc{n}}$ does not change (as the plane is fixed), it moves with $\color{red}{P}$ to always be at the end of a gray line segment from $\color{red}{P}$ that is perpendicular to the plane. This distance from $\color{red}{P}$ to the plane is the length of this gray line segment. This distance is the length of the projection of the vector from $Q$ to $P$ (in purple) onto the normal vector $\color{green}{\vc{n}}$.
The shortest distance from a point to a plane is along a line perpendicular to the plane. Therefore, the distance from point $P$ to the plane is along a line parallel to the normal vector, which is shown as a gray line segment. If we denote by $R$ the point where the gray line segment touches the plane, then $R$ is the point on the plane closest to $P$. The distance from $P$ to the plane is the distance from $P$ to $R$.
To calculate an expression for this distance in terms of the above quantities defining $P$ and the plane, we first calculate an expression for a unit normal vector $\vc{n}$, i.e., a normal vector of length one. It is simply $\vc{N}$ divided by its length: \begin{align*} \vc{n} = \frac{\vc{N}}{\|\vc{N}\|} = \frac{(A,B,C)}{\sqrt{A^2+B^2+C^2}}. \end{align*} The unit normal vector $\vc{n}$ (in green) looks short because in the figure, the $x$, $y$, and $z$ axes each extend from $-5$ to 5.
Let $\vc{v}$ be the vector from $Q$ to $P$ (shown in blue). Since $P=(x_1,y_1,z_1)$ and $Q=(x_0,y_0,z_0)$, we calculate that $\vc{v} = (x_1-x_0, y_1-y_0, z_1-z_0)$. The length of the gray line, i.e., the distance from $P$ to the plane, is simply the length of the projection of $\vc{v}$ onto the unit normal vector $\vc{n}$. Since $\vc{n}$ is length one, this distance is simply the absolute value of the dot product $\vc{v} \cdot \vc{n}$. We'll label the distance $d$; it is \begin{align*} d &= | \vc{v} \cdot \vc{n} |\notag\\ &= | (x_1-x_0, y_1-y_0, z_1-z_0) \cdot \vc{n} |\notag\\ &= \frac{| A(x_1-x_0) +B(y_1-y_0) +C(z_1-z_0)|}{\sqrt{A^2+B^2+C^2}}. \end{align*} This distance is shown on the cyan slider labeled by $d$ to the right of the figure.
Recall that we can also write the equation for the plane as $Ax+By+Cz+D=0$, with $D=-Ax_0-By_0-Cz_0$. We'll substitute into the above formula, to arrive at the following expression for the distance from $P=(x_1,y_1,z_1)$ to the plane $Ax+By+Cz+D=0$: \begin{align*} d = \frac{|Ax_1+By_1+Cz_1 +D|}{\sqrt{A^2+B^2+C^2}}. \end{align*} From this final formula, you can see that the distance didn't depend on the point $Q=(x_0,y_0,z_0)$. As long as $Q$ is in the plane $Ax+By+Cz+D=0$, then we know that $D=-Ax_0-By_0-Cz_0$. The two above formulas for $d$ are equivalent no matter where in the plane $Q$ is. It's clear from the figure how the distance $d$ shouldn't change as you move $Q$ around in the plane. The vector $\vc{v}$ changes, but its projection onto $\vc{n}$ is constant.
You can see an example of using this formula to calculate the distance from a point to a plane.
Thread navigation
Vector algebra
- Previous: A line or a plane or a point?
- Next: Distance from point to plane example
Math 2374
- Previous: A line or a plane or a point?
- Next: Distance from point to plane example