Distance from point to plane example
To illustrate our approach for finding the distance between a point and a plane, we work through an example.
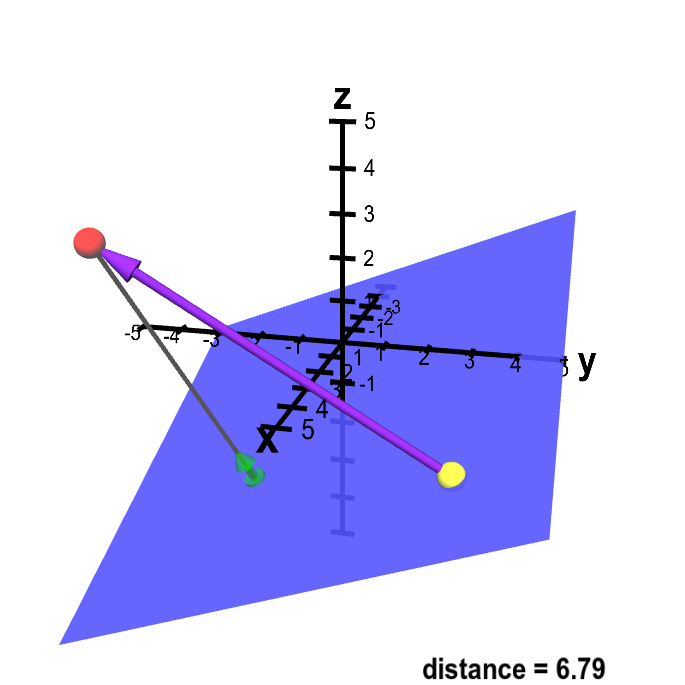
Find the distance from the point $P=(4,-4,3)$ to the plane $2x-2y+5z+8=0$, which is pictured in the below figure in its original view.
Applet loading
Distance from point to plane. A sketch of a way to calculate the distance from point $\color{red}{P}$ (in red) to the plane. The vector $\color{green}{\vc{n}}$ (in green) is a unit normal vector to the plane. You can drag point $\color{red}{P}$ as well as a second point $\vc{Q}$ (in yellow) which is confined to be in the plane. Although the vector $\color{green}{\vc{n}}$ does not change (as the plane is fixed), it moves with $\color{red}{P}$ to always be at the end of a gray line segment from $\color{red}{P}$ that is perpendicular to the plane. This distance from $\color{red}{P}$ to the plane is the length of this gray line segment. This distance is the length of the projection of the vector from $Q$ to $P$ (in purple) onto the normal vector $\color{green}{\vc{n}}$.
Solution: We use the second formula from the page on distance from a point to a plane. From the equation for the plane we substitute $A=2$, $B=-2$, $C=5$, $D=8$. From the point $P$, we substitute $x_1=4$, $y_1=-4$, and $z_1=3$. The distance from $P$ to the plane is \begin{align*} d = \frac{|2 \cdot 4 + (-2)\cdot(-4) + 5 \cdot 3 + 8 |} {\sqrt{2^2+(-2)^2 + 5^2}} = \frac{39}{\sqrt{33}} \approx 6.8 \end{align*}
Thread navigation
Vector algebra
- Previous: Distance from point to plane
- Next: Intersecting planes example
Math 2374
- Previous: Distance from point to plane
- Next: Intersecting planes example