The formula for the dot product in terms of vector components
The geometric definition of the dot product says that the dot product between two vectors $\vc{a}$ and $\vc{b}$ is $$\vc{a} \cdot \vc{b} = \|\vc{a}\| \|\vc{b}\| \cos \theta,$$ where $\theta$ is the angle between vectors $\vc{a}$ and $\vc{b}$. Although this formula is nice for understanding the properties of the dot product, a formula for the dot product in terms of vector components would make it easier to calculate the dot product between two given vectors.
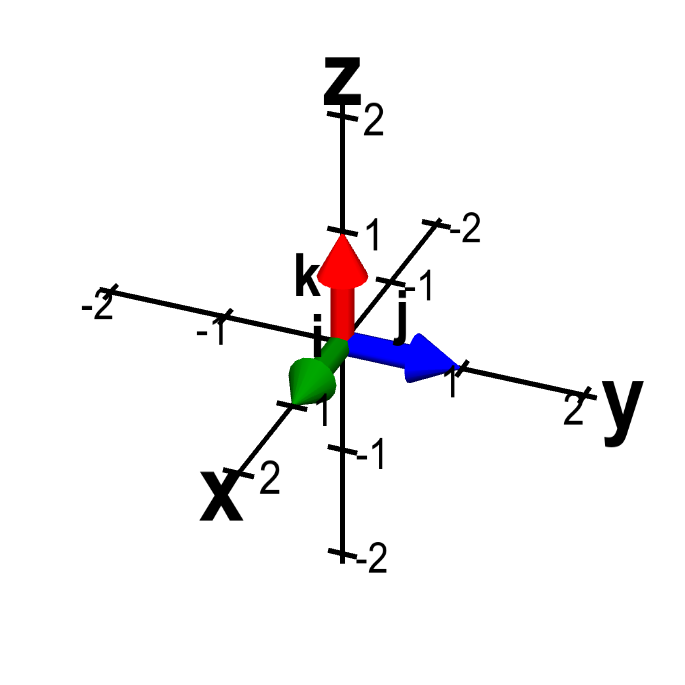
As a first step, we look at the dot product between standard unit vectors, i.e., the vectors $\vc{i}$, $\vc{j}$, and $\vc{k}$ of length one and parallel to the coordinate axes.
Applet loading
The standard unit vectors in three dimensions. The standard unit vectors in three dimensions, $\vc{i}$ (green), $\vc{j}$ (blue), and $\vc{k}$ (red) are length one vectors that point parallel to the $x$-axis, $y$-axis, and $z$-axis respectively. Moving them with the mouse doesn't change the vectors, as they always point toward the positive direction of their respective axis.
Since the standard unit vectors are orthogonal, we immediately conclude that the dot product between a pair of distinct standard unit vectors is zero: \begin{align*} \vc{i} \cdot \vc{j} = \vc{i} \cdot \vc{k} = \vc{j} \cdot \vc{k}=0. \end{align*} The dot product between a unit vector and itself is also simple to compute. In this case, the angle is zero and $\cos\theta=1$. Given that the vectors are all of length one, the dot products are \begin{align*} \vc{i} \cdot \vc{i} = \vc{j} \cdot \vc{j} = \vc{k} \cdot \vc{k}=1. \end{align*}
The second step is to calculate the dot product between two three-dimensional vectors \begin{align*} \vc{a} &= (a_1,a_2,a_3) = a_1\vc{i} + a_2\vc{j}+a_3\vc{k}\\ \vc{b} &= (b_1,b_2,b_3) = b_1\vc{i} + b_2\vc{j}+b_3\vc{k}. \end{align*} To do this, we simply assert that for any three vectors $\vc{a}$, $\vc{b}$, and $\vc{c}$, and any scalar $\lambda$, \begin{align*} (\lambda\vc{a}) \cdot \vc{b} &= \lambda(\vc{a}\cdot\vc{b}) = \vc{a} \cdot (\lambda\vc{b})\\ (\vc{a}+\vc{b}) \cdot \vc{c} &= \vc{a} \cdot \vc{c} + \vc{b}\cdot \vc{c}. \end{align*} (These properties mean that the dot product is linear.)
Given these properties and the fact that the dot product is commutative, we can expand the dot product $\vc{a} \cdot \vc{b}$ in terms of components, \begin{align*} \vc{a} \cdot \vc{b} &= (a_1\vc{i} + a_2\vc{j}+a_3\vc{k}) \cdot (b_1\vc{i} + b_2\vc{j}+b_3\vc{k}) \\ &= a_1b_1 \vc{i} \cdot \vc{i} + a_2b_2\vc{j}\cdot\vc{j} + a_3b_3\vc{k}\cdot\vc{k} \\ &\quad + (a_1b_2+a_2b_1)\vc{i}\cdot\vc{j} + (a_1b_3+a_3b_1)\vc{i}\cdot\vc{k} \\ &\quad + (a_2b_3+a_3b_2)\vc{j}\cdot \vc{k}. \end{align*} Since we know the dot product of unit vectors, we can simplify the dot product formula to \begin{gather} \vc{a} \cdot \vc{b} = a_1b_1+a_2b_2+a_3b_3. \label{dot_product_formula_3d}\tag{1} \end{gather}
Equation \eqref{dot_product_formula_3d} makes it simple to calculate the dot product of two three-dimensional vectors, $\vc{a}, \vc{b} \in \R^3$. The corresponding equation for vectors in the plane, $\vc{a}, \vc{b} \in \R^2$, is even simpler. Given \begin{align*} \vc{a} &= (a_1,a_2) = a_1\vc{i} + a_2\vc{j}\\ \vc{b} &= (b_1,b_2) = b_1\vc{i} + b_2\vc{j}, \end{align*} we can use the same formula, but with $a_3=b_3=0$, \begin{gather} \vc{a} \cdot \vc{b} = a_1b_1+a_2b_2 \label{dot_product_formula_2d}\tag{2}. \end{gather}
Armed with equations \eqref{dot_product_formula_3d} and \eqref{dot_product_formula_2d}, you can make short work of calculating dot products, as shown in these examples.
Thread navigation
Vector algebra
- Previous: The dot product
- Next: Dot product examples
Math 2374
- Previous: The dot product
- Next: Dot product examples