Scalar triple product example

Example

Find the volume of the parallelepiped spanned by the vectors $\vc{a} = (-2,3,1)$, $\vc{b} = (0, 4, 0)$, and $\vc{c} = (-1,3,3)$.

Solution: The volume is the absolute value of the scalar triple product of the three vectors.

The triple product is \begin{align*} (\vc{a} \times \vc{b}) \cdot \vc{c} & =\left| \begin{array}{rrr} -1 & 3 & 3\\ -2 & 3 & 1\\ 0 & 4 & 0 \end{array} \right| \\ &= -1(0-4)- 3 (0-0) +3(-8+0) \\ &= 4-24 = -20 \end{align*} Hence the volume is $|-20| = 20$.

Below is a modified version of the applet used to illustrate the scalar triple product. In this case, the vectors have been fixed to be the values of this example.

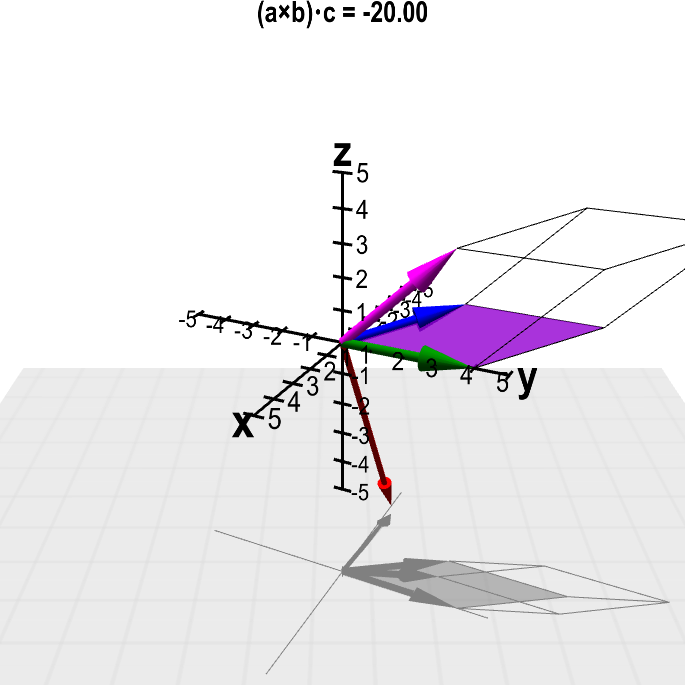
Applet: Scalar triple product with fixed values

Applet loading

Scalar triple product with fixed values. The cyan slider shows the value of the product $(\color{blue}{\vc{a}} \times \color{green}{\vc{b}}) \cdot \color{magenta}{\vc{c}}$, where the vectors $\color{blue}{\vc{a}}$ (in blue), $\color{green}{\vc{b}}$ (in green), and $\color{magenta}{\vc{c}}$ (in magenta) are fixed to given values. The volume of the spanned parallelepiped (outlined) is the magnitude $\|(\color{blue}{\vc{a}} \times \color{green}{\vc{b}}) \cdot \color{magenta}{\vc{c}}\|$. The cross product $\color{blue}{\vc{a}} \times \color{green}{\vc{b}}$ is shown by the red vector. The three-dimensional perspective of this graph is hard to perceive when the graph is still. If you keep the figure rotating by dragging it with the mouse, you'll see it much better.

More information about applet.

Math Insight