Image: Function machine f inverse
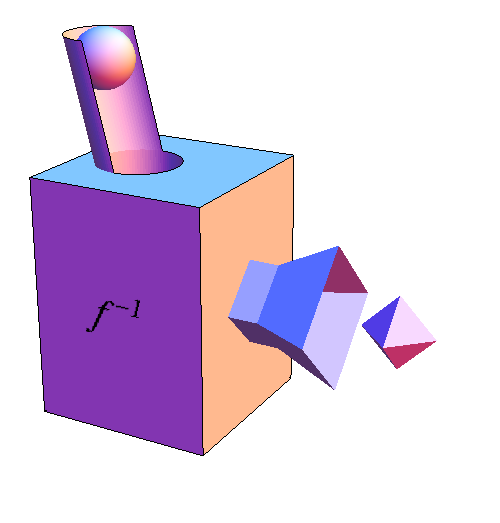
To represent the inverse of a function $f$ with a function machine, we take the function machine for $f$ and run it backwards. We denote the inverse of $f$ by $f^{-1}$. The sphere, which was the output of $f$, becomes the input to $f^{-1}$. As we are running $f$ backwards, the output chute of $f$ becomes an input chute for $f^{-1}$. Similarly, the octahedron, which was the input to $f$, becomes the output of $f^{-1}$, and it comes out of the funnel that used to serve as the input funnel for $f$.
When we run the function machine for $f$ backwards, it will know what to produce for each sphere only if there is only one octahedron that could have produced the sphere when running $f$'s function machine forward. If there are two or more spheres from which $f$'s function machine produces the same octahedron, the backwards function machine won't know which sphere to produce and cannot run. In this case, the inverse of $f$ does not exist.
Image file: function_machine_finv.png
Image links
This image is found in the pages