Math Insight

The derivative of an inverse function

To determine how to compute the derivative of the inverse of $f$, let's think about the derivative of $f$ in terms of the function machine metaphor.

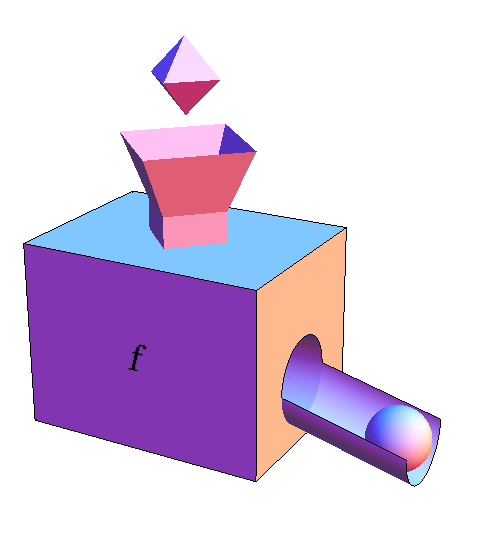
We have denoted the input of $f$ (the tetrahedron) by the variable $x$. Let's denote the output of $f$ (the sphere) by the variable $y$ so that $$y=f(x).$$ Since the derivative of $f$ is the ratio of the change in its output to the change in its input, we can write the derivative as \begin{align*} \diff{f}{x}&=\frac{\text{change in output of $f$}}{\text{change in input to $f$}}\\ &= \frac{\text{change in $y$}}{\text{change in $x$}}. \end{align*}

Can we do the same thing for the inverse of $f$? Let's use a function machine to represent the inverse of $f$.

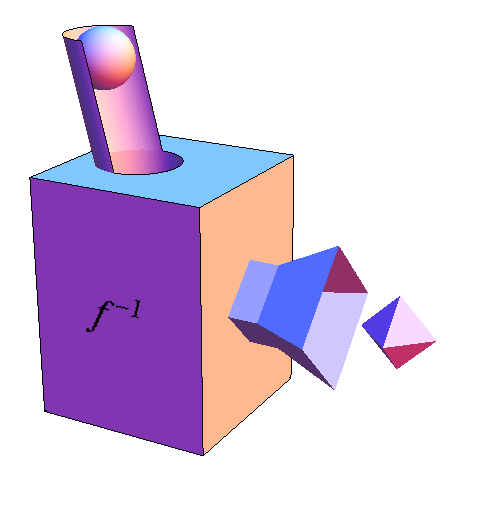
We denote the inverse of $f$ by $f^{-1}$ (pronounced “f inverse”). The input to $f^{-1}$ is the output of $f$ (the sphere), which we have labeled as $y$. The output of $f^{-1}$ is the input to $f$ (the tetrahedron), which we have labeled as $x$. We can write $f^{-1}$ as $$x=f^{-1}(y).$$

We can represent the derivative of $f^{-1}$ in the same was as we did for $f$. Using that the derivative of $f^{-1}$ is the ratio of the change in its output to the change in its input, we can conclude that \begin{align*} \diff{f^{-1}}{y} &=\frac{\text{change in output of $f^{-1}$}}{\text{change in input to $f^{-1}$}}\\ &=\frac{\text{change in input to $f$}}{\text{change in output of $f$}}\\ &= \frac{\text{change in $x$}}{\text{change in $y$}}. \end{align*} In other words, the derivative of $f^{-1}$ is the reciprocal of the derivative of $f$, i.e., the derivative of $f^{-1}(y)$ must be $1/f'(x)$. However, since $f^{-1}(y)$ is a function of $y$ (the sphere) not of $x$ (the tetrahedron), we need to rewrite the derivative of $f^{-1}$ in terms of $y$. The function $x=f^{-1}(y)$ itself is the way to transform $y$ to $x$, so we just need to plug in $f^{-1}(y)$ for $x$ in the expression $1/f'(x)$.

Therefore, the derivative of $f^{-1}(y)$ is \begin{align*} \diff{f^{-1}}{y} &= \frac{1}{f'(f^{-1}(y))}. \end{align*}

An important example where we use this result is to calculate the derivative of the natural logarithm. You can read a version of this page specialized to the derivative of the natural logarithm.