Image: Function machines composed
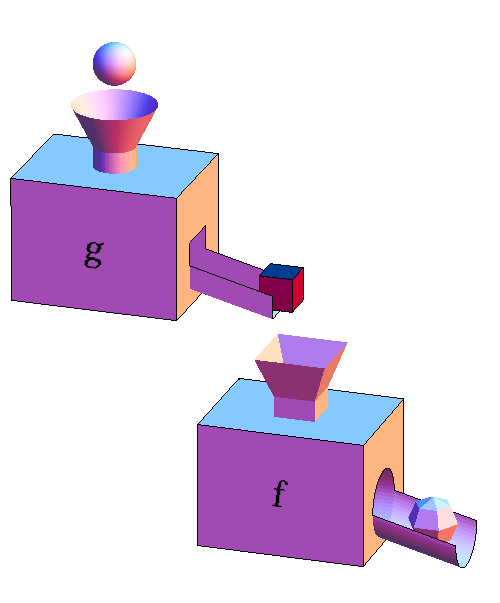
The composition of two functions is represented by a pair of function machines where the output of the first is dumped into the second. The first function machine represents a function $g$ and the second machine represents a function $f$. The composition $f \circ g$ is represented by the combined function whose input is the sphere and output is the faceted ball.
If the sphere represents an input value $x$, then the cube coming out of $g$ represents the output $g(x)$ obtained after applying $g$ to $x$. The cube $g(x)$ is then the input to the second function machine $f$. In response to the cube input, $f$ spits out the faceted ball, which represents $f(g(x))$. The successive application of $g$ and then $f$ to the input $x$ is equivalent to the application of the composition $f \circ g$ to $x$, which we can write as $(f \circ g)(x) = f(g(x))$.
Image file: function_machines_composed.png
Image links
This image is found in the pages