The idea of the chain rule

The chain rule gives us a way to calculate the derivative of a composition of functions, such as the composition $f(g(x))$ of the functions $f$ and $g$. The chain rule can be tricky to apply correctly, especially since, with a complicated expression, one might need to use the chain rule multiple times. Nonetheless, the idea of the chain rule can be understood fairly simply.

The following video outlines the basic idea of the chain rule. In the remainder of this page, we illustrate the idea of the chain rule in three ways. First, we illustrate the concept using function machines. Second, we show how for linear functions, the chain rule is just the product of the slopes of the function graphs. Third, we show that for nonlinear functions, the chain rule is just the product of the slopes of the tangent lines to the function graphs. Examples of the chain rule are given on another page.

Video introduction

The idea of the chain rule.

The chain rule of function machines

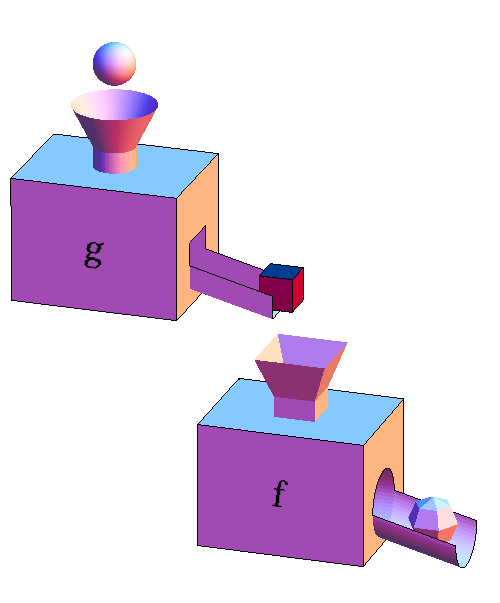
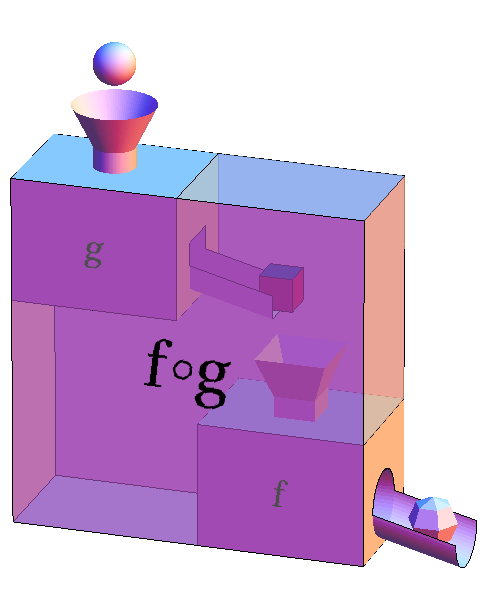
The composition of $f(g(x))$ of two functions $f$ and $g$ can be visualized as hooking up two function machines so that the output of $g$ becomes the input of $f$. Let's call the combined function $h(x)$ so that $h(x)=f(g(x))$. (Sometimes, we write the composition as $h=f \circ g$, so that the large function machine, below, labeled $f \circ g$ illustrates $h$.)

Function machines composed and combined into a new function machine

In the above illustration of function machines, $h$ is the function that transforms the sphere input at the top all the way into the faceted sphere output at the bottom. The input to $h$ is the input to $g$, and the output of $h$ is the output of $f$. The derivative of $h$ tells us how much the output $h$ will change if we change its input a little bit, i.e., it is the ratio of the change in the output of $h$ to the change in its input (equivalently, the ratio of the change in the output of $f$ to the change in the input of $g$). Paraphrasing the limit definition of the derivative, we could write this as \begin{align*} h' &= \lim_{\text{small changes}}\frac{\text{change in output of $h$}}{\text{change in input to $h$}}\\ &= \lim_{\text{small changes}}\frac{\text{change in output of $f$}}{\text{change in input to $g$}}. \end{align*}

The chain rule calculates this derivative by following the chain of events that occur when we change the input to $g$ and observe the resulting change in the output of $f$. A change in the input to $g$ (the sphere) first causes a change in the output of $g$ (the cube). This leads to the same change in the input to $f$ (the same cube), resulting finally in a change in the output of $f$ (the faceted sphere).

In the function machine picture, the derivative of $h$ is the ratio between the change in the faceted sphere to the change in the sphere. The derivative of $g$ is the ratio of the change in the cube to the change in the sphere while the derivative of $f$ is the ratio of the change in the facet sphere to the change in the cube. If we multiply the ratios corresponding to the derivatives of $g$ and $f$, the factors corresponding to the change of the cube cancel, and we obtain the ratio corresponding to the derivative of $h$. If we think of the $d$ from the notation for derivative as denoting “change in,” we can write the result of the chain rule in terms of the function machine inputs and outputs as the following.

In terms of the derivatives of the functions, we can write the chain rule as $$h' = f' \cdot g'.$$ We need to be careful to evaluate the derivatives at the correct points. If we denote the input to $g$ as $x$ (the sphere), then we must evaluate the derivative of $g$ at $x$, using $g'(x)$. Since the input to $g$ is the input to $h$, we must also evaluate the derivative of $h$ as $x$, using $h'(x)$. The sphere (or $x$), however, is not what goes into the $f$ machine. Instead, the cube goes into the $f$ machine. Consequently, we must evaluate the derivative of $f$ at the cube. What is the cube? The cube is the output of the $g$ machine when we put in the sphere (or $x$). The output of $g$ is $g(x)$, so we must evaluate the derivative of $f$ at $g(x)$, using $f'(g(x))$ in our chain rule formula. The resulting chain formula is therefore \begin{gather} h'(x) = f'(g(x))g'(x). \label{chain_rule_formula} \end{gather}

The chain rule for linear functions

The derivative of a function is based on a linear approximation: the tangent line to the graph of the function. For this reason, we can often obtain intuition about the properties of the derivative just by looking at linear functions. The chain rule, in particular, is very simple for linear functions. As we'll see, one important subtlety of the chain rule is absent with linear functions, so they serve as a good starting point to gaining intuition about the chain rule.

The simple form

If $g$ and $f$ are linear functions, we can write them as \begin{align*} g(x) &= ax+b\\ f(x) &= cx + d\\ \end{align*} where $a$, $b$, $c$, and $d$ are parameters determining the slopes and vertical intercepts of the functions. See the left panel of the below applet, where $g$ and $f$ are graphed by the thick blue and thin cyan lines, respectively. The composition of $f$ and $g$ is \begin{align*} h(x) &= f(g(x))\\ &= f(ax +b)\\ &= c(ax+b)+d\\ &= acx + bc+d. \end{align*} The graph of $h$ is a line with slope $ac$ and vertical intercept $bc+d$, graph by the thick green line in the right panel in the below applet.

Since $f$, $g$, and $h$ are linear functions, their derivatives (i.e., the slopes of their tangent lines) are simply equal to the slopes of the lines themselves. In other words, $f'(x)=c$, $g'(x)=a$, and $h'(x)=ac$ independent of the value of $x$. In this case, it's simple to see that the derivative $h'(x)$ is equal to the product of the derivatives $f'$ and $g'$.

In fact, the derivatives don't depend on the intercepts $b$ and $d$, so imagine the special case that $b=d=0$. In this case, $g(x)=ax$ so it multiplies its input $x$ by the slope $a$. The function $f(x)=cx$ multiplies its input by the slope $c$. Finally, in this special case $h$ simpliy multiplies its input by both $a$ and $c$, so its slope is $ac$. What could be simpler? The chain rule simply states that obvious fact that multiplying by $a$ followed by multiplying by $c$ is the same thing as multiplying by the single number $ac$.

Even if $b \ne 0$ or $d \ne 0$, the chain rule isn't much more difficult as those numbers don't affect the slopes. We still just multiply the derivative $a$ by the derivative $c$ to get the derivative of the composition $ac$.

A caution

The reason for the simple form of the chain rule for linear functions is that the derivatives were constants, independent of the value of the inputs to the functions. From experimenting with linear functions, one might falsely assume that the derivative $h'(x)$ of the composition $h(x)=f(g(x))$ might be equal to the product of the derivative $f'(x)$ times the derivative $g'(x)$. The actual chain rule of equation \eqref{chain_rule_formula} has important difference. In using the chain rule, one must be careful to evaluate the derivative of $f$ at $g'(x)$ and use the valid chain rule $h'(x)=f'(g(x))g'(x)$.

The following applet illustrates the chain rule for linear functions. Even though it doesn't make a difference for linear functions, the applet shows graphically the correct points (the green symbols) where one must evaluate the derivatives of $f$ and $g$. If you understand how these points are calculated, then you'll correctly compute the chain rule even for nonlinear functions. Since almost every case where we want to use the chain rule will involve nonlinear functions, evaluating the derivatives at the right points is a crucial step.

The red arrows in the left panel illustrate how to graphically calculate $h(x)=f(g(x))$ where $x=x_0$. The conventions are nearly identical to those one uses for cobwebbing the solution to function iteration.

Starting at the red point for $x_0$, one moves vertically to calculate $g(x_0)$, which would be the height of the point (green diamond) where one hits the graph of $g$. To translate $g(x_0)$ from the vertical axis to the horizontal axis, one must move horizontally to the graph of the diagonal $y=x$. At that point, the value for the horizontal coordinate and vertical coordinate are the same; both coordinates are equal to $g(x_0)$. Then, to calculate $h(x_0)=f(g(x_0))$, one just moves vertically to the graph of $f$. The vertical coordinate of this point (the green triangle) is the required $f(g(x_0))$.

Since to calculate $h(x_0)$, the function $g$ is evaluated at $x_0$ and the function $f$ is evaluated at $g(x_0)$, these are the places where one needs to calculate the derivatives of $g$ and $f$, respectively. Even though the derivative for the case of linear functions doesn't depend on those points, one can still use the applet to remember that $h'(x_0)=f'(g(x_0))g'(x_0).$

The chain rule for linear functions. The linear functions $g(x)=ax+b$ (thick blue line on left) and $f(x)=cx+d$ (thin cyan line on left) are composed to to form the linear function $h(x)=f(g(x))=c(ax+b)+d =cax+cb+d$ (green line on right). For this linear case, the derivatives of $f$, $g$ and $h$ are simply the slopes of the lines: $f'(x)=c$, $g'(x)=a$, and $h'$ is just the product of $f'$ and $g'$: $h'(x)=ac$. In this case of linear functions, the chain rule is quite simple since the slopes are independent of the points where they are evaluated. Nonetheless, to prepare for the nonlinear case where slopes do depend on location, the relevant slopes to calculate $h'(x)$ at $x=x_0$ (represented by the red points on the x-axes) are tracked by the green points on the function graphs. The green point on the graph of $h$ in the right panel illustrates the point on the graph whose height is $h(x_0)$, as labeled on the vertical axis. The left panel illustrates the points on the graphs of $f$ and $g$ that are needed to calculate $h(x_0)=f(g(x_0))$. One first evaluates $g(x_0)$, shown by the green diamond on the graph of $g$. One then evaluates $f(x)$ at $x=g(x_0)$. The value of $g(x_0)$ is the height of the green diamond, as illustrated by the point on the vertical axis. To translate the value of $g(x_0)$ from the vertical to the horizontal axis, one can shift horizontally to the point $(g(x_0),g(x_0))$ on the $x=y$ line (the gray diagonal line). Then one simply moves vertically to the graph of $f$ to calculate $h(x_0)=f(g(x_0))$, which is labeled on the vertical axis. The relevant slopes of $g$ and $f$ are those calculated at the points needed to evaluate $f(g(x_0))$, i.e., the slope of $g$ at $x=x_0$ and the slope of $f$ at $x=g(x_0)$. Therefore, the derivative of $h$ at $x=x_0$ is the product of these slopes: $h'(x_0) = f'(g(x_0)) g'(x_0)$. You can change the parameter values by entering values in the boxes; you can also change $x_0$ by dragging one of the red points on the $x$-axes. You can zoom in, zoom out, or pan the axes by clicking the corresponding buttons.

More information about applet.

The chain rule of nonlinear functions

If you understand the chain rule for linear functions, including where to evaluate the derivative, there isn't much more to understanding the chain rule for nonlinear functions. The only difference is that the tangent line to the graph of a nonlinear function does depend on the point at which you calculate the tangent line. Just as above, if you realize that to calculate $h(x_0)$ one must evaluated $g$ at $x_0$ and $f$ at $g(x_0)$, then it makes sense that $h'(x_0)=f'(g(x_0)) g'(x_0)$.

The following applet uses the same conventions as the above applet. It just is a lot messier than the above linear version because we need to plot the tangent lines which depend on the points where we evaluate the functions. The applet makes it clear that we'd get the wrong answer if we examined the slope of $f$ at $x_0$ rather than $g(x_0)$. The applet doesn't show the wrong tangent line with slope $f'(x_0)$ (that would make it too confusing). But you can see that the function $f$ does in general have a different slope above the point $x_0$ than it does at the green triangle.

The chain rule as multiplying slopes. The chain rule for the derivative of the composition $h(x)=f(g(x))$ of two functions $f$ and $g$ can be thought of as the product of the tangent line slopes. The trick is to evaluate the slopes at the correct points of the functions $f$ and $g$. The correct points, illustrated by the green symbols on the function graphs, are those where the functions are evaluated to compute $f(g(x))$. To calculate the composition $h(x)$ at $x=x_0$ (red dots on $x$-axis of the both panels), one must first evaluate $g$ at $x=x_0$, as illustrated by the green diamond on the graph of $g$ (thick blue curve in the left panel). Next, one evaluates $f$ at $g(x_0)$. To graphically translate the value of $g(x_0)$ from the vertical axis to the horizontal axis, one shifts horizontally from the green diamond to the line $x=y$ (gray line), arriving at the point $(g(x_0),g(x_0))$. By moving vertically to the graph of $f$ (thin cyan curve), one obtains $f(g(x_0))$, which is the vertical coordinate of the green triangle. In the graph of the composition $h(x)=f(g(x))$ (green curve in right panel), calculating $h(x_0)$ simply corresponds to moving vertically from the red point representing $x_0$ to the green circle on the graph of $h$, yielding the vertical coordinate $h(x_0)$. The slope of the tangent line at the green circle on the graph of $h$, is simply the product of the slope of $g$'s tangent line at the green diamond and the slope of $f$'s tangent line at the green triangle, just as in the case of linear functions. The slopes are shown near the green symbols, and the tangent lines are shown as thin lines of the same color as the function graphs. Therefore, the chain rule formula for the derivative of $h$ evaluated at $x=x_0$ is: $h'(x_0)=f'(g(x_0))g'(x_0)$. You can change the functions and $x_0$ by entering expressions in the boxes; you can also change $x_0$ by dragging one of the red points on the $x$-axes. You can zoom in, zoom out, or pan the axes by clicking the corresponding buttons.

More information about applet.

This page focused exclusively on the idea of the chain rule. Of course, knowing the general idea and accurately using the chain rule are two different things. If you are new to the chain rule, check out some simple chain rule examples. If you want to see some more complicated examples, take a look at the chain rule page from the Calculus Refresher.

Math Insight