Math Insight

Function machine composition

The composition of two functions $f$ and $g$ is the function formed by taking the output of the function $g$ and using that as the input to the function $f$. If we represent both $f$ and $g$ as function machines, the composition would look like the following figure.

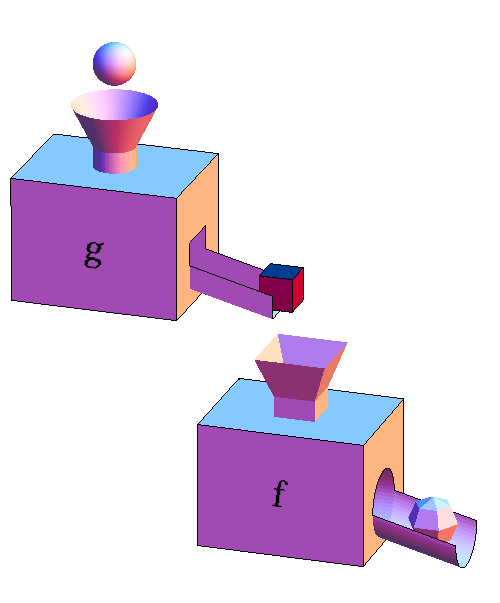
The function machine metaphor makes clear one important condition for a composition to work. Whatever comes out of the output chute of $g$ had better be able to fit into the input funnel of $f$. In this case, $g$ spits out cubes and $f$ takes in cubes, so the composition works. In mathematical terms, we need to make sure that the range of $g$ is contained in the domain of $f$. Otherwise, the composition isn't defined; the output of $g$ would get stuck in the funnel of $f$, and we'd have a disastrous result.

If the variable $x$ represents the input to the function $g$ (the sphere), then its output (the cube) would be $g(x)$. Then, we use the cube $g(x)$ as the input to $f$ so that its output (the faceted ball) is $f(g(x))$.

We recommend using the formula $f(g(x))$ to think about the composition of $f$ and $g$, as there is no ambiguity in the order in which you apply the functions. It is clear that $g(x)$ is the input to $f$. Sometimes, though, we want to denote the composed function itself without any reference to its input $x$. In this case, we use the notation $f \circ g$. The function $f \circ g$ is represented by the large function machine whose input is the sphere (the input to $g$) and whose output is the faceted ball (the output of $f$).

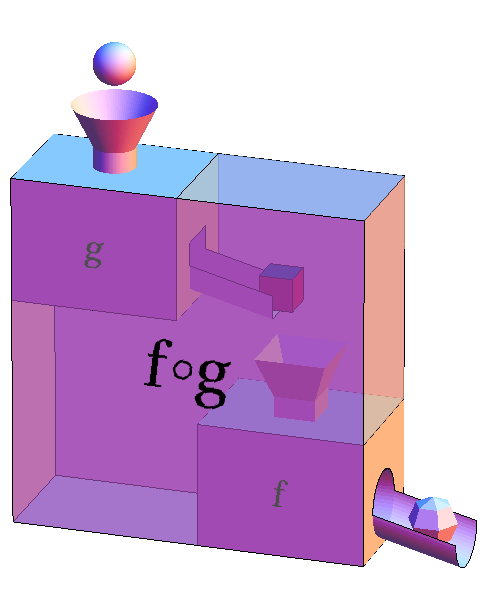
The challenge with the notation $f \circ g$ is that it is hard to correctly remember which function is applied first. The order is backwards of what you might think. The notation $f \circ g$ means you apply $g$ first and then $f$. If we take the function $f \circ g$, and put in the input $x$, the function machine will spit out $f(g(x))$, which we can write as $(f \circ g)(x) = f(g(x))$. You can see why we recommend sticking with the $f(g(x))$ notation if you can.

To further explore how function composition works, you can check out some examples.