Image: Polar coordinates
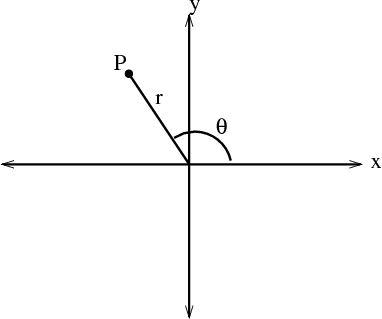Illustration of the definition of polar coordinates $r$, $\theta$ of a point $P$. The coordinate $\theta$ is the angle between the positive $x$-axis and the line from the origin to $P$. The coordinate $r$ is the distance from $P$ to the origin.
Image file: polar_coordinates.png
Image links
This image is found in the pages