Cylindrical coordinates

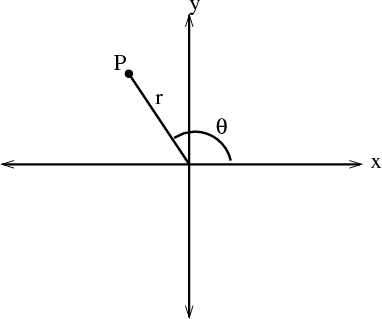
Cylindrical coordinates are a simple extension of the two-dimensional polar coordinates to three dimensions. Recall that the position of a point in the plane can be described using polar coordinates $(r,\theta)$. The polar coordinate $r$ is the distance of the point from the origin. The polar coordinate $\theta$ is the angle between the $x$-axis and the line segment from the origin to the point. Polar coordinates are illustrated in the below figure and described more in another page.

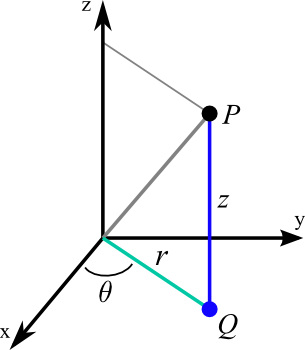
Cylindrical coordinates simply combine the polar coordinates in the $xy$-plane with the usual $z$ coordinate of Cartesian coordinates. To form the cylindrical coordinates of a point $P$, simply project it down to a point $Q$ in the $xy$-plane (see the below figure). Then, take the polar coordinates $(r,\theta)$ of the point $Q$, i.e., $r$ is the distance from the origin to $Q$ and $\theta$ is the angle between the positive $x$-axis and the line segment from the origin to $Q$. The third cylindrical coordinate is the same as the usual $z$-coordinate. It is the signed distance of the point $P$ to the $xy$-plane (being negative is $P$ is below the $xy$-plane). The below figure illustrates the cylindrical coordinates $(r,\theta,z)$ of the point $P$.

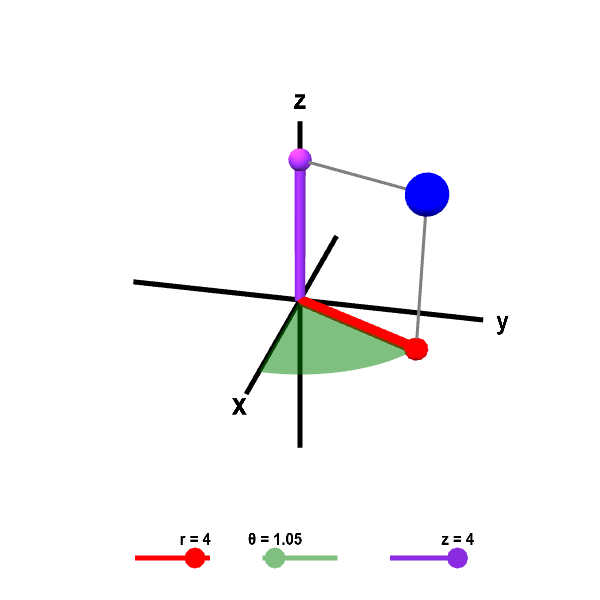
You can further explore the properties of the cylindrical coordinates with the follow applet. You can observe how changing the coordinates $(r,\theta,z)$ changes the position of the point $P$. Just as with polar coordinates, we usually limit $0 \le \theta < 2\pi$ and $r \ge 0$ to descrease the non-uniqueness of cylindrical coordinates. However, when $r=0$, there is a non-uniqueness since the point $P$ is on the $z$ axis when $r=0$, independent of the value of $\theta$.

The Java applet did not load, and the above is only a static image representing one view of the applet. The applet was created with LiveGraphics3D. The applet is not loading because it looks like you do not have Java installed. You can click here to get Java.

Cylindrical coordinates. Given the values for cylindrical coordinates $r$, $\theta$, and $z$, which you can change by dragging the blue points on the sliders, the large purple point shows the corresponding position in Cartesian coordinates. The blue point is the projection of the purple point in the $xy$-plane. This projection gives perspective and helps in visualizing $\theta$ and $r$. The coordinate $r$ is the length of the cyan line segment from the origin to the blue point. The coordinate $\theta$ is the angle the cyan line segment makes with the positive $x$-axis. The coordinate $z$ is the same as the $z$-coordinate of Cartesian coordinates. On the sliders, $\theta$ is written as $\Theta$.