Math Insight

Single autonomous differential equation problems

 

Problem 1

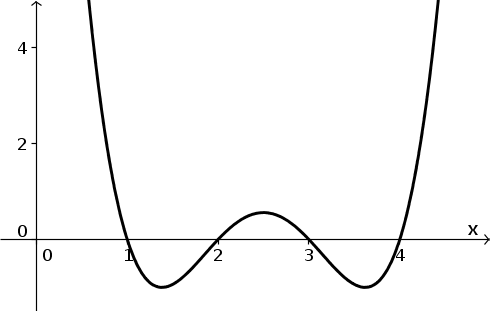
For the differential equation \begin{align*} \diff{x}{t} = f(x), \end{align*} the function $f(x)$ is graphed below.

  1. Sketch the vector field illustrating the rate of change $\diff{x}{t}$.
  2. Find the equilibria and calculate their stability.
  3. Graph the solution $x(t)$
    1. for initial condition $x(0)=3.8$.
    2. for initial condition $x(0)=4.2$.
Autonomous differential equation example function 1

Problem 2

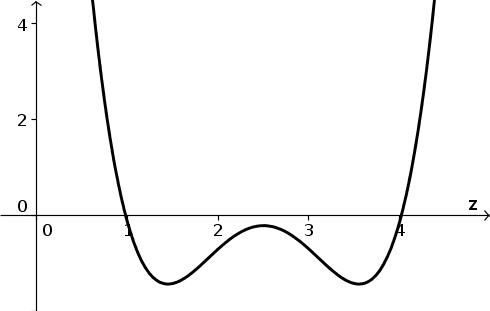
For the differential equation \begin{align*} \diff{z}{t} = h(z), \end{align*} the function $h(z)$ is graphed below.

  1. Sketch the vector field illustrating the rate of change $\diff{z}{t}$.
  2. Find the equilibria and calculate their stability.
  3. Graph the solution $z(t)$
    1. for initial condition $z(0)=3.8$.
    2. for initial condition $z(0)=4.2$.
Autonomous differential equation example function 2

Problem 3

Consider the dynamical system \begin{align*} \diff{y}{t} = 3(y-2)(y-1)(y+1). \end{align*}

  1. Find the equilibria and use the stability theorem to calculate their stability.
  2. Sketch the vector field illustrating the rate of change $\diff{y}{t}$.
  3. Graph the solution $y(t)$
    1. for the initial conditions $y(0)=1.5$.
    2. for the initial conditions $y(0)=2$.
    3. for the initial conditions $y(0)=2.5$.

Problem 4

Consider the differential equation \begin{align*} \diff{z}{t} = -3(z-5)(z-10). \end{align*}

  1. Find the equilibria and use the stability theorem to calculate their stability.
  2. Sketch the vector field illustrating the rate of change $\diff{y}{t}$.
  3. Graph the solution $z(t)$
    1. for the initial conditions $z(0)=0$.
    2. for the initial conditions $z(0)=8$.
    3. for the initial conditions $z(0)=12$.

Problem 5

For the differential equation \begin{align*} \diff{q}{t} = e^{-q^2-3q+1} \end{align*} find the equilibria and use the stability theorem to calculate their stability. Graph the solution for the initial condition $q(0)=0$.

Problem 6

For the dynamical system \begin{align*} \diff{r}{t} = -re^{r} \end{align*} find the equilibria and use the stability theorem to calculate their stability. Graph the solution for the initial condition $r(0)=5$.

Problem 7

Estimate the solution of the differential equation \begin{align*} \diff{m}{t} &= e^{-m^2}\\ m(0) &= -1, \end{align*} using the Forward Euler algorithm. Use a time step $\Delta t= 1$ to estimate $m(3)$.

Problem 8

Estimate the solution of the dynamical system \begin{align*} \diff{w}{t} &= 1-e^{-w}\\ w(0) &= -1, \end{align*} using the Forward Euler algorithm. Use a time step $\Delta t= 0.5$ to estimate $w(2)$.

Problem 9

Consider the dynamical system \begin{align*} \diff{u}{t} = u(2-u). \end{align*}

  1. Using any valid method, determine the equilibria of the dynamical system and their stability.
  2. Graph of the solution of the dynamical system with initial condition $u(0)=0.8$.
  3. Use the Forward Euler algorithm with time step $\Delta t=2$ to estimate the solution with initial condition $u(0)=0.8$. Take four time steps, estimating $u(2)$, $u(4)$, $u(6)$, and $u(8)$. Does the behavior of the solution estimated by Forward Euler match your previous results? If not, how is the behavior different?
  4. Use the Forward Euler algorithm with time step $\Delta t=1$ to estimate the solution with initial condition $u(0)=0.8$. Take four time steps, estimating $u(1)$, $u(2)$, $u(3)$ and $u(4)$. Does the behavior of the solution estimated by Forward Euler match your previous results? If not, how is the behavior different?
  5. Use the Forward Euler algorithm with time step $\Delta t=0.5$ to estimate the solution with initial condition $u(0)=0.8$. Take four time steps, estimating $u(1/2)$, $u(1)$, $u(3/2)$ and $u(2)$. Does the behavior of the solution estimated by Forward Euler match your previous results? If not, how is the behavior different?

One you have worked on a few problems, you can compare your solutions to the ones we came up with.

Similar pages