Two dimensional autonomous differential equation problems

Problem 1

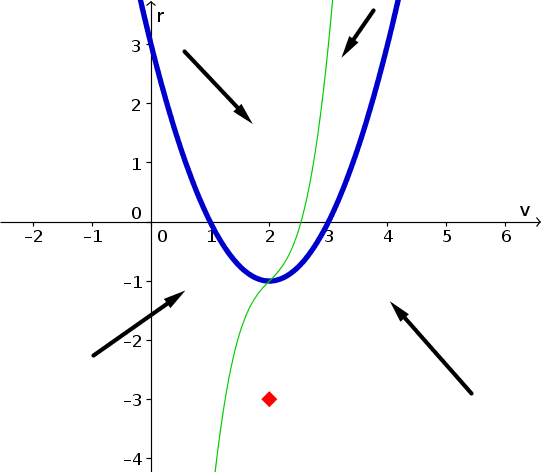
Consider the two-dimensional system of autonomous differential equations \begin{align*} \diff{v}{t} &= f(v,r)\\ \diff{r}{t} &= g(v,r), \end{align*} where $f$ and $g$ are some functions. The nullclines of this system are plotted in the below phase plane, where $v$ is plotted on the horizontal axis and $r$ is plotted on the vertical axis. The $v$-nullcline is plotted by the thin green line; the $g$-nullcline is plotted by the thick blue line. The nullclines divide the phase plane into four regions. In each of those regions, directions arrows are shown indicating the general direction of the flow of solution trajectories in the region. The direction arrows indicate whether the state variables ($v$ and $r$) increase or decrease in the region.

Along each segment of each nullcline, draw a direction arrow indicating the direction of solution trajectories that cross the nullcline.
Identify all equilbria by indicating their position in the phase plane and estimating the values of $v$ and $r$ at each equilibrium.
Imagine that the initial condition was $(v(0),r(0))=(2,-3)$, as shown by the red diamond. Sketch in the phase plane a plausible solution of the differential equations with that initial condition. You should should be consistent with all the information given and what you determined.
Sketch how this solution might look like when plotted versus time. Plot a curve for both $v(t)$ and $r(t)$ where you use $t$ for the horizontal axis. You solution simply needs to be consistent with the solution you sketched in the phase plane.

Problem 2

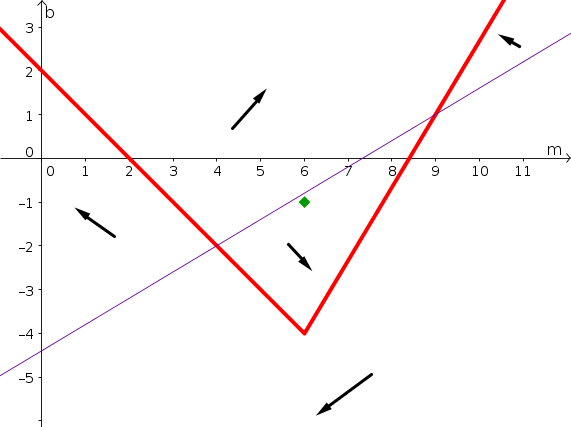
Consider the two-dimensional system of autonomous differential equations \begin{align*} \diff{m}{t} &= h(m,b)\\ \diff{b}{t} &= k(m,b), \end{align*} where $h$ and $k$ are some functions. The nullclines of this system are plotted in the below phase plane, where $m$ is plotted on the horizontal axis and $b$ is plotted on the vertical axis. The $m$-nullcline is plotted by the thick red line; the $b$-nullcline is plotted by the thin purple line. The nullclines divide the phase plane into five regions. In each of those regions, directions arrows are shown indicating the general direction of the flow of solution trajectories in the region. The direction arrows indicate whether the state variables ($m$ and $b$) increase or decrease in the region.

Along each segment of each nullcline, draw a direction arrow indicating the direction of solution trajectories that cross the nullcline.
Identify all equilbria by indicating their position in the phase plane and estimating the values of $m$ and $b$ at each equilibrium.
Imagine that the initial condition was $(m(0),b(0))=(6,-1)$, as shown by the green diamond. Sketch in the phase plane a plausible solution of the differential equations with that initial condition. You should should be consistent with all the information given and what you determined.
Sketch how this solution might look like when plotted versus time. Plot a curve for both $m(t)$ and $b(t)$ where you use $t$ for the horizontal axis. You solution simply needs to be consistent with the solution you sketched in the phase plane.

Problem 3

Consider the two-dimensional system of autonomous differential equations \begin{align*} \diff{w}{t} &= -w-u + 1\\ \diff{u}{t} &= w-u +1 \end{align*}

Find the nullclines and sketch them on the phase plane. Be sure to label your axes and the nullclines.
Identify all equilbria. Give their values and show them in the phase plane.
Sketch a direction arrow in each of the regions of the phase plane divided by the nullclines.
Sketch a direction arrow on each segment of each nullcline.
Sketch a plausible solution in the phase plane starting at the initial condition $(w(0),u(0))=(0,0)$ that is consistent with your direction arrows.
Sketch a plausible solution of $w(t)$ and $u(t)$ versus time $t$ that corresponds to your sketch in the phase plane.
Estimate the solution $w(t)$ and $u(t)$ with initial conditions $(w(0),u(0))=(0,0)$ using three steps of the Forward Euler algorithm with time step $\Delta t = 1$.

Problem 4

Consider the two-dimensional system of autonomous differential equations \begin{align*} \diff{z}{t} &= z+v - 1\\ \diff{v}{t} &= z-v +1 \end{align*}

Find the nullclines and sketch them on the phase plane. Be sure to label your axes and the nullclines.
Identify all equilbria. Give their values and show them in the phase plane.
Sketch a direction arrow in each of the regions of the phase plane divided by the nullclines.
Sketch a direction arrow on each segment of each nullcline.
Sketch a plausible solution in the phase plane starting at the initial condition $(z(0),v(0))=(0,0)$ that is consistent with your direction arrows.
Sketch a plausible solution of $z(t)$ and $v(t)$ versus time $t$ that corresponds to your sketch in the phase plane.
Estimate the solution $z(t)$ and $v(t)$ with initial conditions $(z(0),v(0))=(0,0)$ using three steps of the Forward Euler algorithm with time step $\Delta t = 1$.

Problem 5

Find the equilibria of the following system of differential equations: \begin{align*} \diff{a}{t} &= a(1-a+b)\\ \diff{b}{t} &= b(1-b+a). \end{align*}

Problem 6

Find the equilibria of the following system of differential equations: \begin{align*} \diff{p}{t} &= p(1-p-q)\\ \diff{q}{t} &= q(2-p-q). \end{align*}

Problem 7

For the following system of differential equations, plot the nullclines and find the equilibria. \begin{align*} \diff{r}{t} &= -r(2-s)\\ \diff{s}{t} &= s(3-r). \end{align*} Plot direction arrows and a plausible solution in the phase plane for the initial conditions $r(0)=1$ and $s(0)=1$.

Problem 8

For the following system of differential equations, plot the nullclines and find the equilibria. \begin{align*} \diff{u}{t} &= -u(v-2)\\ \diff{v}{t} &= v(3-u). \end{align*} Plot direction arrows and a plausible solution in the phase plane for the initial conditions $u(0)=1$ and $v(0)=1$.

One you have worked on a few problems, you can compare your solutions to the ones we came up with.

Math Insight