Solutions to two dimensional autonomous differential equation problems

Problem 1

The direction arrows on the nullclines are green vertical and horizontal arrows in the following plot.
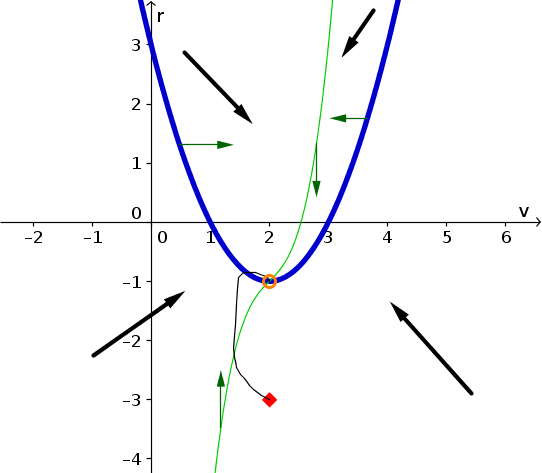
The one equilibrium is identified by the orange circle around the one point where the nullclines intersect. Its coordinates are $(v,r)=(2,-1)$.
A plausible solution for initial condition $(v(0),r(0))=(2,-3)$ is shown by the black curve starting at the initial conditions (red diamond). Initially, the curve must move upward and to the left, as given by the direction arrow. It must cross the $v$-nullcline moving straight up and then begin to move upward and to the right. When it reaches the $r$-nullcline, it must cross it moving straight right and then begin moving downward and to the right. At this point, the direction arrows don't completely determine what must happen. In the above figure, the solution is shown heading straight to the equilibrium (orange circle). (It is also theoretically possible that the solution crosses the $v$-nullcline again and moves downward and to the left before getting to the equilibrium.)
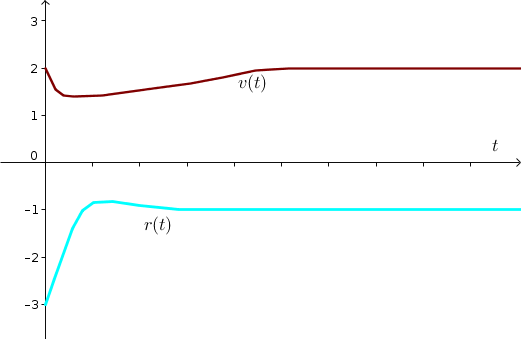
The following graph is a possibility of how $v(t)$ and $r(t)$ could look like as a function of time. The temporal scale is comletely arbitrary because the phase plane does not include information about time. The important features are the following: $v$ starts at $2$ and $r$ starts at $-3$; $v(t)$ initially decreases then increases back to 2; $r(t)$ initially increases, overshoots $-1$ by a little bit, then comes back down to $-1$.

Problem 2

The direction arrows on the nullclines are green vertical and horizontal arrows in the following plot.
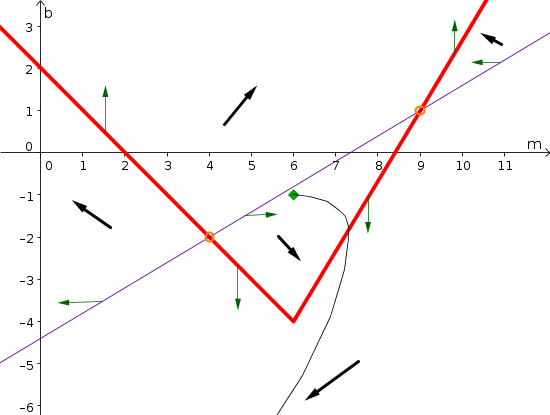
The two equilibria are identified by the orange circles around the points where the nullclines intersect. Their coordinates are $(4,-2)$ and $(9,1)$.
A plausible solution for initial condition $(m(0),b(0))=(6,-1)$ is shown by the black curve starting at the initial conditions (green diamond). Since $m(t)$ is increasing and $b(t)$ is decreasing, the solution trajectory initially moves downward and to the right. When it crosses the $m$-nullcline, it moves straight downward as the rate of change of $m$ is zero at this point. Aftewards, the trajectory moves downward and to the left, as both $m$ and $b$ are decreasing.
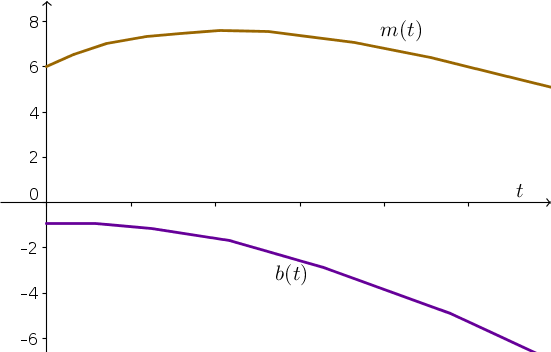
The following graph is a possibility of how $m(t)$ and $b(t)$ could look like as a function of time. The temporal scale is comletely arbitrary because the phase plane does not include information about time. The important features are the following: $m$ starts at $6$ and $b$ starts at $-1$; $m(t)$ initially increases then decreases; $b(t)$ decreases the whole time. After $b(t)$ drops below $-6$, the solution left the displayed portion of the phase plane, so we don't have more information about what happens.

Problem 3

The $w$-nullcline is the line $-w-u+1=0$ or $w+u=1$. It is the thin blue line plotted in the below phase plane. The $u$-nullcline is the line $w-u+1=0$ or $u-w=1$, which is the thick green line plotted below.
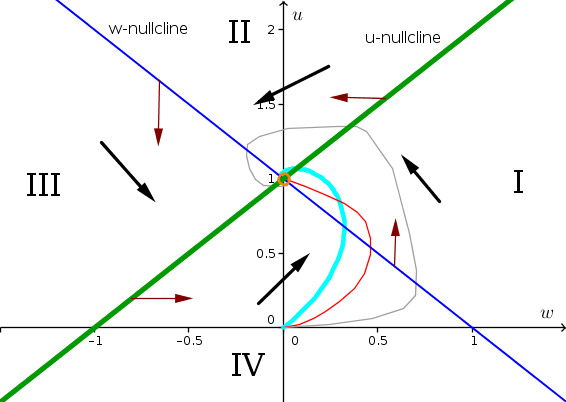
There is one equilibrium where the nullclines intersect. It is at the point $(w,u) = (0,1)$. One can also determine the value by solving system of two equations. By adding the equations $w+u=1$ and $u-w=1$, one gets $2u=2$ or $u=1$. Plugging that value into either of the original equations, gives $w=0$. The equilibrium is shown by the orange circle on the phase plane.
We label the four regions of the phase plane by I, II, III, and IV, as shown in the graph. To determine the direction arrows in each region, we pick a point and look to see if $w$ and $u$ are increasing and decreasing.
1. In region I, we pick the point $(w,u) = (1,1)$. Then $\diff{w}{t}=-1-1+1=-1 \lt 0$ so $w$ is decreasing, and $\diff{u}{t} = 1-1+1=1 \gt 0$ so $u$ is increasing. We draw the arrow pointing upward and to the left.
2. In region II, we pick the point $(w,u) = (0,2)$. Then $\diff{w}{t} = 0-2+1=-1 \lt 0$ and $\diff{u}{t} = 0 -2+1=-1 \lt 0$. Both $w$ and $u$ are decreasing and we draw the arrow pointing downward and to the left.
3. In region III, we pick the point $(w,u) = (-1, 1)$. Then, $\diff{w}{t} = 1-1+1=1 \gt 0$ and $\diff{u}{t} = -1-1+1 \lt 0$. We draw the direction arrow downward and to the right since $w$ is increasing and $u$ is decreasing.
4. In region IV, we pick the point $(w,u)= (0,0)$. Then, $\diff{w}{t} = 1 \gt 0 $ and $\diff{u}{t} = 1 \gt 0$. Both $w$ and $u$ are increasing, and we draw the direction arrow pointing upward and to the right.
On the $w$-nullcline (thin blue line), we know that $\diff{w}{t}=0$, so there can be no horizontal movement. The direction arrow must point straight up or straight down. The left segment of the $w$-nullclines is between regions II and III. In both those regions $u$ is decreasing and the arrows point downward. The arrow on the left part of the nullcline must point straight down. In constrast, the right segment of the the $w$-nullcline is between regions I and IV, where $u$ is increasing. The direction arrow must point upward. For the $u$-nullcline (thick green line), the arrows must point left or right since $\diff{u}{t}=0$. The right segment is between regions I and II, where $w$ is decreasing. We draw the arrow straight left. The left segment of the $u$-nullcline is between regions III and IV, where $w$ is increasing. We draw the arrow straight to the right.
The direction arrows spiral in a counterclockwise motion around the equilibrium $(0,1)$. For this case, when you follow the direction arrows, you are forced to spiral inwards toward the equilibrium. But, there's no way to know how much you spiral around. You can take your pick of how you want it to look. The red curve is a good choice, because it is the simplest. The actual solution looks like the cyan curve (but we know this only because we could use an applet to see what really happens). A more complicated solution would be the gray curve. For simplicity, let's imagine the we chose the red curve for our trajectory.
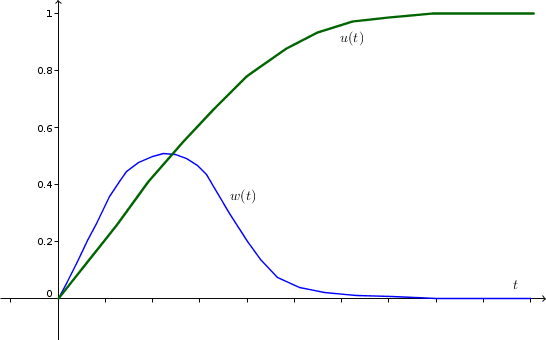
To plot the red curve as functions $w(t)$ and $u(t)$ versus time, we just need to observe that $w(t)$ increases from zero to about 0.5 and then decreases back to 0. On the other hand, $u(t)$ increases from zero to one monotonically. The resulting curves are sketched below.
Using Forward Euler with $\Delta t =1$, we calculate $w(1)$ and $u(1)$ from $w(0)=0$ and $u(0)=0$. \begin{align*} w(1) &\approx w(0) + \Delta t (-w(0)-u(0) + 1)\\ &= 0 + 1(-0- 0 + 1) = 1\\ u(1) &\approx u(0) + \Delta t (w(0)-u(0) + 1)\\ &= 0 + 1(0-0+1)= 1 \end{align*} We calculate $w(2)$ and $u(2)$ from $w(1)=1$ and $u(1)=1$. \begin{align*} w(2) &\approx w(1) + \Delta t (-w(1)-u(1) + 1)\\ &= 1 + 1(-1- 1 + 1) = 0\\ u(2) &\approx u(1) + \Delta t (w(1)-u(1) + 1)\\ &= 1 + 1(1-1+1)= 2 \end{align*} We calculate $w(3)$ and $u(3)$ from $w(2)=0$ and $u(2)=2$. \begin{align*} w(3) &\approx w(2) + \Delta t (-w(2)-u(2) + 1)\\ &= 0 + 1(-0- 2 + 1) = -1\\ u(3) &\approx u(2) + \Delta t (w(2)-u(2) + 1)\\ &= 2+ 1(0-2+1)= 1 \end{align*} With this Forward Euler approximation, we are spiralling around counterclockwise (though we aren't moving inward).

Problem 4

The $z$-nullcline is $z+v-1=0$ or $z+v=1$, It is the thin blue line plotted in the below phase plane. The $v$-nullcline is the line $z-v+1=0$ or $v-z=1$, which is the thick green line plotted below.
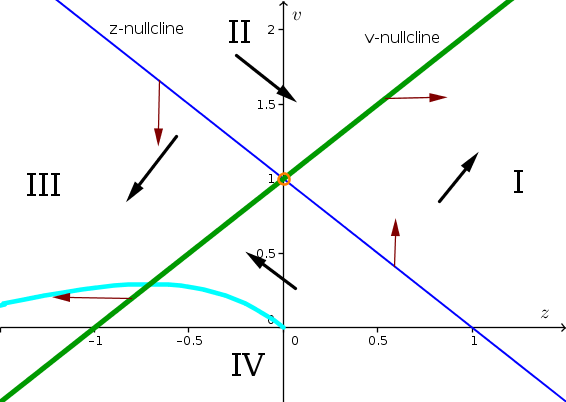
There is one equilibrium where the nullclines intersect. It is at the point $(z,v) = (0,1)$. One can also determine the value by solving system of two equations. By adding the equations $z+v=1$ and $v-z=1$, one gets $2v=2$ or $v=1$. Plugging that value into either of the original equations, gives $z=0$. The equilibrium is shown by the orange circle on the phase plane.
We label the four regions of the phase plane by I, II, III, and IV, as shown in the graph. To determine the direction arrows in each region, we pick a point and look to see if $z$ and $v$ are increasing and decreasing.
1. In region I, we pick the point $(z,v) = (1,1)$. Then $\diff{z}{t}=1+1-1=1 \gt 0$ so $z$ is increasing, and $\diff{v}{t} = 1-1+1=1 \gt 0$ so $v$ is increasing. We draw the arrow pointing upward and to the right.
2. In region II, we pick the point $(z,v) = (0,2)$. Then $\diff{z}{t} = 0+2-1=1 \gt 0$ and $\diff{v}{t} = 0 -2+1=-1 \lt 0$. We draw the direction arrow downward and to the right since $z$ is increasing and $v$ is decreasing
3. In region III, we pick the point $(z,v) = (-1, 1)$. Then, $\diff{z}{t} = -1+1-1=-1 \lt 0$ and $\diff{v}{t} = -1-1+1 \lt 0$. Both $z$ and $v$ are decreasing and we draw the arrow pointing downward and to the left.
4. In region IV, we pick the point $(z,v)= (0,0)$. Then, $\diff{z}{t} = -1 \gt 0 $ and $\diff{u}{t} = 1 \gt 0$. Since $z$ is decreasing and $v$ is increasing, we we draw the direction arrow pointing upward and to the left.
On the $z$-nullcline (thin blue line), we know that $\diff{z}{t}=0$, so there can be no horizontal movement. The direction arrow must point straight up or straight down. The left segment of the $z$-nullclines is between regions II and III. In both those regions $v$ is decreasing and the arrows point downward. The arrow on the left part of the nullcline must point straight down. In constrast, the right segment of the the $z$-nullcline is between regions I and IV, where $v$ is increasing. The direction arrow must point upward. For the $v$-nullcline (thick green line), the arrows must point left or right since $\diff{v}{t}=0$. The right segment is between regions I and II, where $z$ is increasing. We draw the arrow straight right. The left segment of the $v$-nullcline is between regions III and IV, where $z$ is decreasing. We draw the arrow straight to the left.
Starting at $(z(0),v(0))=(0,0)$, the solution must move upward and to the left and cross the $v$-nullcline moving straight left. The it moves downward and to the left. One such solution trajectory is the the cyan curve shown above.
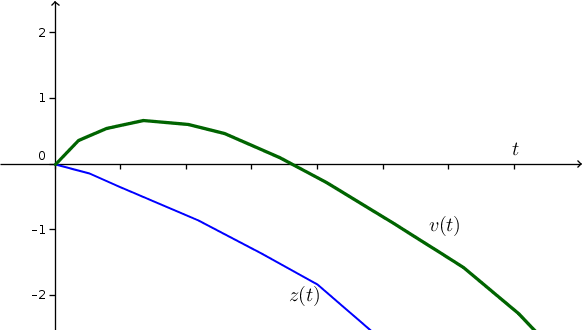
To plot the cyan curve as functions $z(t)$ and $v(t)$ versus time, we just need to observe that $z(t)$ decreases along the trajectory while $v(t)$ initially increases to about 0.5 before decreasing. increases from zero to about 0.5 and then decreases back to 0. The resulting curves are sketched below.
Using Forward Euler with $\Delta t =1$, we calculate $z(1)$ and $v(1)$ from $z(0)=0$ and $v(0)=0$. \begin{align*} z(1) &\approx z(0) + \Delta t (z(0)+v(0) - 1)\\ &= 0 + 1(0+ 0 - 1) = -1\\ v(1) &\approx v(0) + \Delta t (z(0)-v(0) + 1)\\ &= 0 + 1(0-0+1)= 1 \end{align*} We calculate $z(2)$ and $v(2)$ from $z(1)=-1$ and $v(1)=1$. \begin{align*} z(2) &\approx z(1) + \Delta t (z(1)+v(1) - 1)\\ &= -1 + 1(-1 + 1 - 1) = -2\\ v(2) &\approx v(1) + \Delta t (z(1)-v(1) + 1)\\ &= 1 + 1(-1-1+1)= 0 \end{align*} We calculate $z(3)$ and $v(3)$ from $z(2)=-2$ and $v(2)=0$. \begin{align*} z(3) &\approx z(2) + \Delta t (z(2)+v(2) - 1)\\ &= -2 + 1(-2+0 + 1) = -3\\ v(3) &\approx v(2) + \Delta t (z(2)-v(2) + 1)\\ &= 0+ 1(-2-0+1)= -1 \end{align*}

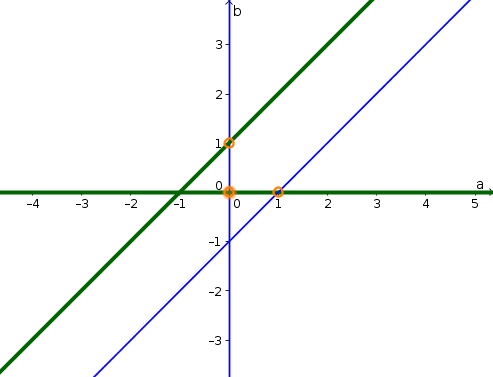
The equilibrium values of $a$ and $b$ must simultaneous satisfy $0 = \diff{a}{t}= a(1-a+b)$ (the $a$-nullcline) and $0 = \diff{b}{t}=b(1-b+a)$ (the $b$-nullcline). In other words, one of the conditions \begin{align*} a = 0 \quad \text{or} \quad 1-a+b=0 \end{align*} must be satified (so that $\diff{a}{t}=0$) as well as one of the conditions \begin{align*} b = 0 \quad \text{or} \quad 1-b+a=0 \end{align*} must be satisfied (so that $\diff{b}{t}=0$). We need to find all combinations $(a,b)$ that satisfy both conditions

If we set $a=0$, then the first condition is satified. If we simultaneously set $b=0$, then the second condition is satisfied. Therefore $(a,b)=(0,0)$ is one equilibrium.

If we set $a=0$, then the first condition is satified. If we simultaneously set $0 = 1-b+a = 1-b+0$, then the second condition is satisfied. Since this last equation is $b=1$, we determine that another equilibrium is $(a,b)=(0,1)$.

These are all the equilibria when $a=0$. Now, we pick the second option for the first condition and set $1-a+b=0$. We can satisfy the second condition by setting $b=0$. Then the first equation becomes $0=1-a+b = 1-a$ or $a=1$. Another equilibrium is $(a,b)=(1,0)$.

If we satisfy the first condition with $1-a+b=0$ and the second condition with $1-b+a=0$, we can attempt to solve the system of equations by adding the two equations. The result is $2=0$, which has no solutions. There are no more equilibria.

The equilibria are shown by the orange circles in the below phase plane plot. The thin blue lines are the $a$-nullcline and the thick green lines are the $b$-nullcline.

Problem 6

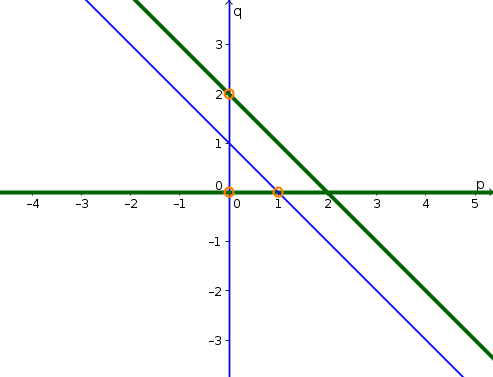
The equilibrium values of $p$ and $q$ must simultaneous satisfy $0 = \diff{p}{t}= p(1-p-q)$ (the $p$-nullcline) and $0 = \diff{q}{t}=q(2-p-q)$ (the $q$-nullcline). In other words, one of the conditions \begin{align*} p= 0 \quad \text{or} \quad 1-p-q=0 \end{align*} must be satified (so that $\diff{q}{t}=0$) as well as one of the conditions \begin{align*} q = 0 \quad \text{or} \quad 2-p-q=0 \end{align*} must be satisfied (so that $\diff{q}{t}=0$). We need to find all combinations $(p,q)$ that satisfy both conditions

If we set $p=0$, then the first condition is satified. If we simultaneously set $q=0$, then the second condition is satisfied. Therefore $(p,q)=(0,0)$ is one equilibrium.

If we set $p=0$, then the first condition is satified. If we simultaneously set $0 = 2-p-q = 2-0-q$, then the second condition is satisfied. Since this last equation is $q=2$, we determine that another equilibrium is $(p,q)=(0,2)$.

These are all the equilibria when $p=0$. Now, we pick the second option for the first condition and set $1-p-q=0$. We can satisfy the second condition by setting $q=0$. Then the first equation becomes $0=1-p-q = 1-p$ or $p=1$. Another equilibrium is $(p,q)=(1,0)$.

If we satisfy the first condition with $1-p-q=0$ and the second condition with $2-p-q=0$, we can attempt to solve the system of equations by subtracting the two equations. The result is $1=0$, which has no solutions. There are no more equilibria.

The equilibria are shown by the orange circles in the below phase plane plot. The thin blue lines are the $p$-nullcline and the thick green lines are the $q$-nullcline.

Problem 7

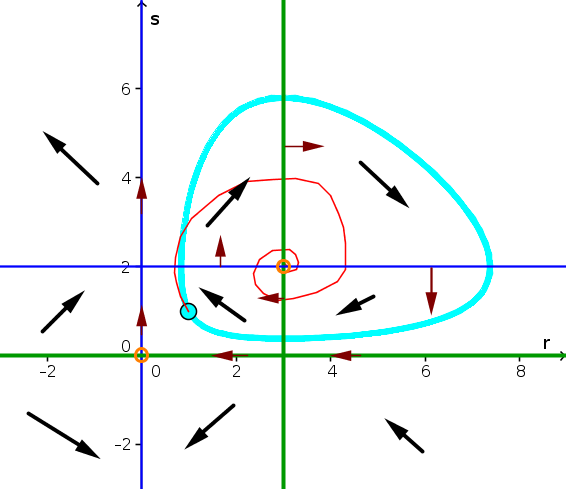
The $r$-nullcline is composed of the lines $r=0$ and $s=2$, which are shown by the thin blue lines in the phase plane plot below. The $s$-nullcline is composed othe lines $s=0$ and $r=2$, which are shown by the thick green lines below. The equilibrium are the two points where they cross: $(r,s)=(0,0)$ and $(r,s)=(3,2)$. The equilibria are shown by the orange circles.

By plugging in test points, one can determine the direction arrows in the different regions of the phase plane. In the region where $r$ and $s$ are positive, the direction arrows show spiralling around the equilibrium $(r,s)=(3,2)$. Starting at the initial condition $(r(0),s(0))=(1,1)$, the direction arrows plotted aren't enough for one to determine exactly how the solution behaves. It could, for example, spiral in a circle (cyan curve) or spiral toward the equilibrium (red curve). The important point is that whatever curve one chooses, it must be consistent with the direction arrows.

Problem 8

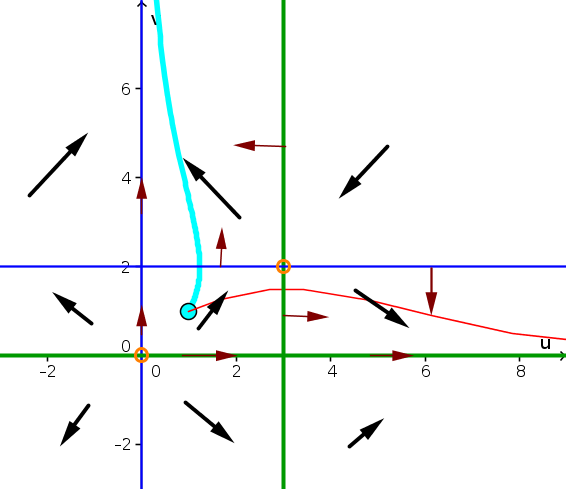
The $u$-nullcline is composed of the lines $u=0$ and $v=2$, which are shown by the thin blue lines in the phase plane plot below. The $v$-nullcline is composed othe lines $v=0$ and $u=2$, which are shown by the thick green lines below. The equilibrium are the two points where they cross: $(u,v)=(0,0)$ and $(u,v)=(3,2)$. The equilibria are shown by the orange circles.

By plugging in test points, one can determine the direction arrows in the different regions of the phase plane. Starting at the initial condition $(u(0),u(0))=(1,1)$, the trajectory must first move upward and to the right unless it cross the $u$-nullcline, at which point it moves upward and to the left. A trajectory consistent with the direction arrows is shown by the cyan curve.

Math Insight