The formula for the cross product
The geometric definition of the cross product is good for understanding the properties of the cross product. However, the geometric definition isn't so useful for computing the cross product of vectors. For computations, we will want a formula in terms of the components of vectors. We start by using the geometric definition to compute the cross product of the standard unit vectors.
Cross product of unit vectors
Let $\vc{i}$, $\vc{j}$, and $\vc{k}$ be the standard unit vectors in $\R^3$. (We define the cross product only in three dimensions. Note that we are assuming a right-handed coordinate system.)

Applet loading
The standard unit vectors in three dimensions. The standard unit vectors in three dimensions, $\vc{i}$ (green), $\vc{j}$ (blue), and $\vc{k}$ (red) are length one vectors that point parallel to the $x$-axis, $y$-axis, and $z$-axis respectively. Moving them with the mouse doesn't change the vectors, as they always point toward the positive direction of their respective axis.
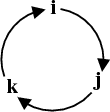
The parallelogram spanned by any two of these standard unit vectors is a unit square, which has area one. Hence, by the geometric definition, the cross product must be a unit vector. Since the cross product must be perpendicular to the two unit vectors, it must be equal to the other unit vector or the opposite of that unit vector. Looking at the above graph, you can use the right-hand rule to determine the following results. \begin{align*} \vc{i} \times \vc{j} &= \vc{k}\\ \vc{j} \times \vc{k} &=\vc{i}\\ \vc{k} \times \vc{i} &= \vc{j} \end{align*} This little cycle diagram can help you remember these results.
What about $\vc{i} \times \vc{k}$? By the right-hand rule, it must be $-\vc{j}$. By remembering that $\vc{b} \times \vc{a} = - \vc{a} \times \vc{b}$, you can infer that \begin{align*} \vc{j} \times \vc{i} &= -\vc{k}\\ \vc{k} \times \vc{j} &= -\vc{i}\\ \vc{i} \times \vc{k} &= -\vc{j}. \end{align*}
Finally, the cross product of any vector with itself is the zero vector ($\vc{a} \times \vc{a}=\vc{0}$). In particular, the cross product of any standard unit vector with itself is the zero vector.
General vectors
With the exception of the two special properties mentioned above ($\vc{b} \times \vc{a} = -\vc{a} \times \vc{b}$, and $\vc{a} \times \vc{a} = \vc{0}$), we'll just assert that the cross product behaves like regular multiplication. It obeys the following properties:
- $(y\vc{a}) \times \vc{b} = y(\vc{a} \times \vc{b}) = \vc{a} \times (y\vc{b})$,
- $\vc{a} \times (\vc{b}+\vc{c}) = \vc{a} \times \vc{b} + \vc{a} \times \vc{c}$,
- $(\vc{b}+\vc{c}) \times \vc{a} = \vc{b} \times \vc{a} + \vc{c} \times \vc{a}$,
where $\vc{a}$, $\vc{b}$, and $\vc{c}$ are vectors in $R^3$ and $y$ is a scalar. (These properties mean that the cross product is linear.) We can use these properties, along with the cross product of the standard unit vectors, to write the formula for the cross product in terms of components.
We write the components of $\vc{a}$ and $\vc{b}$ as: \begin{align*} \vc{a} = (a_1,a_2,a_3)= a_1 \vc{i} + a_2 \vc{j} + a_3 \vc{k}\\ \vc{b} = (b_1,b_2,b_3)= b_1 \vc{i} + b_2 \vc{j} + b_3 \vc{k} \end{align*}
First, we'll assume that $a_3=b_3=0$. (Then, the manipulations are much easier.) We calculate: \begin{align*} \vc{a} \times \vc{b} &= (a_1 \vc{i} + a_2 \vc{j}) \times (b_1 \vc{i} + b_2 \vc{j})\\ &= a_1b_1 (\vc{i}\times\vc{i}) + a_1b_2(\vc{i} \times \vc{j}) + a_2b_1 (\vc{j} \times \vc{i}) + a_2b_2 (\vc{j} \times \vc{j}) \end{align*} Since we know that $\vc{i} \times \vc{i}= \vc{0}= \vc{j} \times \vc{j}$ and that $\vc{i} \times \vc{j} = \vc{k} = -\vc{j} \times \vc{i}$, this quickly simplifies to \begin{align*} \vc{a} \times \vc{b} &= (a_1b_2-a_2b_1) \vc{k}\\ &= \left| \begin{array}{cc} a_1 & a_2\\ b_1 & b_2 \end{array} \right| \vc{k}. \end{align*} Writing the result as a determinant, as we did in the last step, is a handy way to remember the result.
The general case where $a_3$ and $b_3$ aren't zero is a bit more complicated. However, it's just a matter of repeating the same manipulations above using the cross product of unit vectors and the properties of the cross product.
We start with by expanding out the product \begin{align*} \vc{a} \times \vc{b} &= (a_1 \vc{i} + a_2 \vc{j} + a_3\vc{k}) \times (b_1 \vc{i} + b_2 \vc{j} + b_3\vc{k})\\ &= a_1b_1 (\vc{i}\times\vc{i}) + a_1b_2(\vc{i} \times \vc{j}) + a_1b_3(\vc{i} \times \vc{k})\\ &\quad + a_2b_1 (\vc{j} \times \vc{i}) + a_2b_2 (\vc{j} \times \vc{j}) + a_2b_3 (\vc{j} \times \vc{k})\\ &\quad + a_3b_1 (\vc{k} \times \vc{i}) + a_3b_2 (\vc{k} \times \vc{j}) + a_3b_3 (\vc{k} \times \vc{k}) \end{align*} and then calculate all the cross products of the unit vectors \begin{align*} \vc{a} \times \vc{b} &= a_1b_2 \vc{k} - a_1b_3 \vc{j} - a_2b_1 \vc{k} + a_2b_3 \vc{i} + a_3b_1 \vc{j} - a_3b_2 \vc{i}\\ &= (a_2b_3-a_3b_2 )\vc{i} - (a_1b_3-a_3b_1) \vc{j} +(a_1b_2-a_2b_1) \vc{k}. \end{align*} Using determinants, we can write the result as \begin{align*} \vc{a} \times \vc{b} &=\left| \begin{array}{cc} a_2 & a_3\\ b_2 & b_3 \end{array} \right| \vc{i} - \left| \begin{array}{cc} a_1 & a_3\\ b_1 & b_3 \end{array} \right| \vc{j} + \left| \begin{array}{cc} a_1 & a_2\\ b_1 & b_2 \end{array} \right| \vc{k}. \end{align*}
Looking at the formula for the $3 \times 3$ determinant, we see that the formula for a cross product looks a lot like the formula for the $3 \times 3$ determinant. If we allow a matrix to have the vector $\vc{i}$, $\vc{j}$, and $\vc{k}$ as entries (OK, maybe this doesn't make sense, but this is just as a tool to remember the cross product), the $3 \times 3$ determinant gives a handy mnemonic to remember the cross product: \begin{align*} \vc{a} \times \vc{b} = \left| \begin{array}{ccc} \vc{i} & \vc{j} & \vc{k}\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{array} \right|. \end{align*} This is a compact way to remember how to compute the cross product.
Thread navigation
Vector algebra
- Previous: The cross product
- Next: Cross product examples
Math 2374
- Previous: The cross product
- Next: Cross product examples
Similar pages
- The cross product
- The formula for the dot product in terms of vector components
- The dot product
- The scalar triple product
- Cross product examples
- Dot product examples
- Vectors in two- and three-dimensional Cartesian coordinates
- The relationship between determinants and area or volume
- An introduction to vectors
- Scalar triple product example
- More similar pages