The dot product
The dot product between two vectors is based on the projection of one vector onto another. Let's imagine we have two vectors $\vc{a}$ and $\vc{b}$, and we want to calculate how much of $\vc{a}$ is pointing in the same direction as the vector $\vc{b}$. We want a quantity that would be positive if the two vectors are pointing in similar directions, zero if they are perpendicular, and negative if the two vectors are pointing in nearly opposite directions. We will define the dot product between the vectors to capture these quantities.
But first, notice that the question “how much of $\vc{a}$ is pointing in the same direction as the vector $\vc{b}$” does not have anything to do with the magnitude (or length) of $\vc{b}$; it is based only on its direction. (Recall that a vector has a magnitude and a direction.) The answer to this question should not depend on the magnitude of $\vc{b}$, only its direction. To sidestep any confusion caused by the magnitude of $\vc{b}$, let's scale the vector so that it has length one. In other words, let's replace $\vc{b}$ with the unit vector that points in the same direction as $\vc{b}$. We'll call this vector $\vc{u}$, which is defined by $$\vc{u} = \frac{\vc{b}}{\|\vc{b}\|}.$$
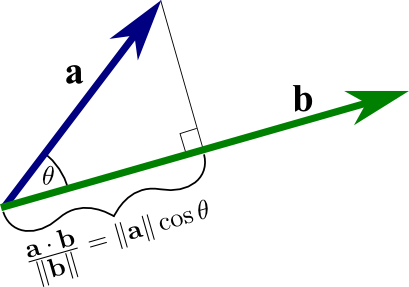
The dot product of $\vc{a}$ with unit vector $\vc{u}$, denoted $\vc{a} \cdot \vc{u}$, is defined to be the projection of $\vc{a}$ in the direction of $\vc{u}$, or the amount that $\vc{a}$ is pointing in the same direction as unit vector $\vc{u}$. Let's assume for a moment that $\vc{a}$ and $\vc{u}$ are pointing in similar directions. Then, you can imagine $\vc{a} \cdot \vc{u}$ as the length of the shadow of $\vc{a}$ onto $\vc{u}$ if their tails were together and the sun was shining from a direction perpendicular to $\vc{u}$. By forming a right triangle with $\vc{a}$ and this shadow, you can use geometry to calculate that \begin{gather}\vc{a} \cdot \vc{u} = \|\vc{a}\| \cos \theta, \label{dot_product_unit} \end{gather} where $\theta$ is the angle between $\vc{a}$ and $\vc{u}$.
If $\vc{a}$ and $\vc{u}$ were perpendicular, there would be no shadow. That corresponds to the case when $\cos \theta = \cos \pi/2 =0$ and $\vc{a} \cdot \vc{u}=0$. If the angle $\theta$ between $\vc{a}$ and $\vc{u}$ were larger than $\pi/2$, then the shadow wouldn't hit $\vc{u}$. Since in this case $\cos \theta <0$, the dot product $\vc{a} \cdot \vc{u}$ is also negative. You could think of $-\vc{a} \cdot \vc{u}$ (which is positive in this case) as being the length of the shadow of $\vc{a}$ on the vector $-\vc{u}$, which points in the opposite direction of $\vc{u}$.
But we need to get back to the dot product $\vc{a}\cdot \vc{b}$, where $\vc{b}$ may have a magnitude different than one. This dot product $\vc{a}\cdot \vc{b}$ should depend on the magnitude of both vectors, $\|\vc{a}\|$ and $\|\vc{b}\|$, and be symmetric in those vectors. Hence, we don't want to define $\vc{a}\cdot \vc{b}$ to be exactly the projection of $\vc{a}$ on $\vc{b}$; we want it to reduce to this projection for the case when $\vc{b}$ is a unit vector. We can accomplish this very easily: just plug the definition $\vc{u}=\frac{\vc{b}}{\|\vc{b}\|}$ into our dot product definition of equation \eqref{dot_product_unit}. This leads to the definition that the dot product $\vc{a} \cdot \vc{b}$, divided by the magnitude $\|\vc{b}\|$ of $\vc{b}$, is the projection of $\vc{a}$ onto $\vc{b}$. $$\frac{\vc{a}\cdot \vc{b}}{\|\vc{b}\|} = \|\vc{a}\| \cos\theta.$$ Then, if we multiply by through by $\|\vc{b}\|$, we get a nice symmetric definition for the dot product $\vc{a} \cdot \vc{b}$. \begin{gather} \vc{a}\cdot \vc{b} = \|\vc{a}\| \|\vc{b}\|\cos\theta. \label{dot_product_definition}\tag{2} \end{gather}
The picture of the geometric interpretation of $\vc{a} \cdot \vc{b}$ is almost identical to the above picture for $\vc{a} \cdot \vc{u}$. We just have to remember that we have to divide through by $\|\vc{b}\|$ to get the projection of $\vc{a}$ onto $\vc{b}$.
In the following interactive applet, you can explore this geometric intrepretation of the dot product, and observe how it depends on the vectors and the angle between them. (The reported number shouldn't depend on the length of $\|\vc{b}\|$ since we divided by that magnitude.)
The dot product as projection. The dot product of the vectors $\vc{a}$ (in blue) and $\vc{b}$ (in green), when divided by the magnitude of $\vc{b}$, is the projection of $\vc{a}$ onto $\vc{b}$. This projection is illustrated by the red line segment from the tail of $\vc{b}$ to the projection of the head of $\vc{a}$ on $\vc{b}$. You can change the vectors $\vc{a}$ and $\vc{b}$ by dragging the points at their ends or dragging the vectors themselves. Notice how the dot product is positive for acute angles and negative for obtuse angles. The reported number does not depend on $\|\vc{b}\|$ only because we've divided through by that magnitude.
The geometric definition of equation \eqref{dot_product_definition} makes the properties of the dot product clear. One can see immediately from the formula that the dot product $\vc{a}\cdot\vc{b}$ is positive for acute angles and negative for obtuse angles. The formula demonstrates that the dot product grows linearly with the length of both vectors and is commutative, i.e., $\vc{a} \cdot \vc{b} = \vc{b} \cdot \vc{a}$.
However, the geometric formula \eqref{dot_product_definition} is not convenient for calculating the dot product when we are given the vectors $\vc{a}$ and $\vc{b}$ in terms of their components. To facilitate such calculations, we derive a formula for the dot product in terms of vector components. With such formula in hand, we can run through examples of calculating the dot product.
Thread navigation
Vector algebra
- Previous: Examples of n-dimensional vectors
- Next: The formula for the dot product in terms of vector components
Math 2374
Similar pages
- The formula for the dot product in terms of vector components
- Dot product examples
- The cross product
- The formula for the cross product
- Cross product examples
- The scalar triple product
- Scalar triple product example
- The zero vector
- Multiplying matrices and vectors
- Matrix and vector multiplication examples
- More similar pages