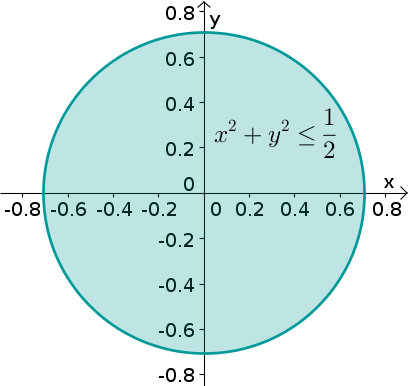Triple integral examples
Example 1
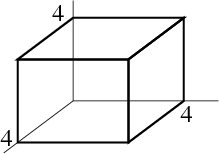
A cube has sides of length 4. Let one corner be at the origin and the adjacent corners be on the positive $x$, $y$, and $z$ axes.
If the cube's density is proportional to the distance from the xy-plane, find its mass.
Solution: The density of the cube is $f(x,y,z) = kz$ for some constant $k$.
If $\dlv$ is the cube, the mass is the triple integral \begin{align*} \iiint_\dlv kz\,dV &= \int_0^4 \int_0^4 \int_0^4 kz\,dx\,dy\,dz\\ &= \int_0^4 \int_0^4 \left(\left.kxz \right|_{x=0}^{x=4}\right) dy\,dz\\ &= \int_0^4 \int_0^4 4 k z \,dy\,dz\\ &= \int_0^4 \left(\left. 4kzy \right|_{y=0}^{y=4}\right) dz\\ &= \int_0^4 16 kz dz = \left.\left.8kz^2\right|_{z=0}^{z=4}\right. = 128k \end{align*}
If distance is in cm and $k=1$ gram per cubic cm per cm, then the mass of the cube is 128 grams.
Example 2
Evaluate the integral \begin{align*} \int_0^1 \int_0^x \int_0^{1+x+y} f(x,y,z) dz \, dy\, dx \end{align*} where $f(x,y,z)=1$.
Solution: \begin{align*} &\int_0^1 \int_0^x \int_0^{1+x+y} dz \, dy\, dx\\ &\qquad= \int_0^1 \int_0^x \left(z\Big|_{z=0}^{z=1+x+y}\right)dy\, dx\\ &\qquad= \int_0^1 \int_0^x (1+x+y) dy\, dx\\ &\qquad= \int_0^1 \biggl[y + yx + \frac{y^2}{2}\biggr]_{y=0}^{y=x} dx\\ &\qquad= \int_0^1 \biggl(x + x^2 + \frac{x^2}{2}\biggr) dx\\ &\qquad= \int_0^1 \biggl(x + \frac{3x^2}{2} \biggr) dx\\ &\qquad= \biggl[\frac{x^2}{2} + \frac{x^3}{2} \biggr]_0^1 = \frac{1}{2} + \frac{1}{2} = 1 \end{align*}
Note: when we integrate $f(x,y,z)=1$, the integral $\iiint_\dlv dV$ is the volume of the solid $\dlv$.
Example 3a
Set up the integral of $f(x,y,z)$ over $\dlv$, the solid “ice cream cone” bounded by the cone $z=\sqrt{x^2+y^2}$ and the half-sphere $z = \sqrt{1-x^2-y^2}$, pictured below.
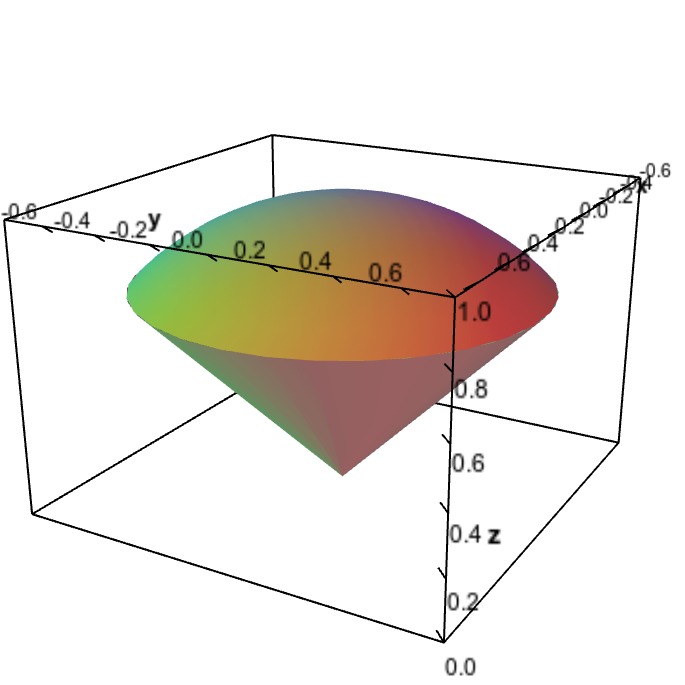
Applet loading
Ice cream cone region. The ice cream cone region is bounded above by the half-sphere $z=\sqrt{1-x^2-y^2}$ and bounded below by the cone $z=\sqrt{x^2+y^2}$.
Solution: We'll use the shadow method to set up the bounds on the integral. This means we'll write the triple integral as a double integral on the outside and a single integral on the inside of the form \begin{gather*} \iint_{\textit{shadow}} \int_{\textit{bottom}}^{\textit{top}} f(x,y,z). \end{gather*} We'll let the $z$-axis be the vertical axis so that the cone $z=\sqrt{x^2+y^2}$ is the bottom and the half-sphere $z = \sqrt{1-x^2-y^2}$ is the top of the ice cream cone $\dlv$. Hence, $\dlv$ is the region between these two surfaces: \begin{align} \sqrt{x^2+y^2} \le z \le \sqrt{1-x^2-y^2}. \label{zinequalities} \end{align} These inequalities give the range of $z$ as a function of $x$ and $y$ and thus form the bounds of the inner integral, which will be an integral with respect to $z$ of the form \begin{gather*} \int_{\textit{bottom}}^{\textit{top}} f(x,y,z)dz= \int_{\sqrt{x^2+y^2}}^{\sqrt{1-x^2-y^2}} f(x,y,z)dz. \end{gather*}
The whole region $\dlv$ is the set of points satisfying the inequalities \eqref{zinequalities} while $x$ and $y$ range over the shadow of the ice cream cone that is parallel to the $xy$-plane, as illustrated by the cyan circle below.
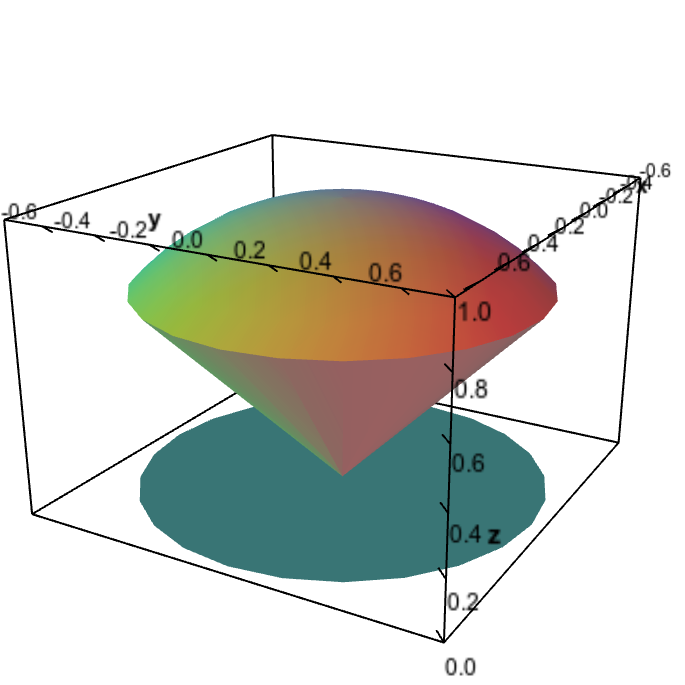
Applet loading
Ice cream cone region with shadow. The ice cream cone region is bounded above by the half-sphere $z=\sqrt{1-x^2-y^2}$ and bounded below by the cone $z=\sqrt{x^2+y^2}$. The two surfaces intersect along a circle defined by $x^2+y^2=1/2$ and $z=1/\sqrt{2}$, which is the widest part of the ice cream cone. Therefore, the shadow of the ice cream cone region parallel to the $xy$-plane is the disk of radius $1/\sqrt{2}$ described by $x^2+y^2 \le 1/2$.
The shadow parallel to the $xy$-plane is the maximal range of $x$ and $y$ over all points inside $\dlv$. Inside the ice cream cone, the maximal range of $x$ and $y$ occurs where the two surfaces meet, i.e., where the “ice cream” (the half-sphere) meets the cone. From the figure, you can see that the surfaces meet in a circle, and the range of $x$ and $y$ is the disk that is the interior of that circle.
The surfaces meet when $ \sqrt{x^2+y^2} = \sqrt{1-x^2-y^2}$, which means $x^2+y^2 = 1-x^2-y^2$ or \begin{align*} x^2+y^2 = \frac{1}{2}. \end{align*} In other words, for any point $(x,y,z)$ in the ice cream cone, the inequality \begin{align} x^2+y^2 \le \frac{1}{2} \label{shadow} \end{align} is satisfied. This inequality describes the shadow of the ice cream cone, which is the set of points $(x,y)$ that lie in a disk of radius $1/\sqrt{2}$, as illustrated below.
Now we've reduced the rest of the task of finding bounds for the triple integral to the much simpler task of finding bounds for a double integral over the shadow described by inequality \eqref{shadow}. We'll let $y$ be the inner integral of the double integral, meaning we need to describe the range of $y$ in the shadow as a function of $x$. To do this, we simply rewrite inequality \eqref{shadow} in terms of $y$ as \begin{align*} -\sqrt{1/2 - x^2} \le y \le \sqrt{1/2 - x^2}. \end{align*} This range of $y$ as a function of $x$ gives the bounds on the inner integral of the double integral.
Finally, for the bounds on the outer integral, we need the maximal range of $x$ alone. Given that $x^2+y^2 \le 1/2$, the maximal range occurs when $y=0$ so that $x^2 \le 1/2$. We can write the maximal range of $x$ is \begin{align*} -1/\sqrt{2} \le x \le 1/\sqrt{2}. \end{align*} The double integral with respect to $x$ and $y$ becomes \begin{gather*} \iint_{\textit{shadow}} \cdots dy\,dx = \int_{-1/\sqrt{2}}^{1/\sqrt{2}} \int_{-\sqrt{1/2-x^2}}^{\sqrt{1/2-x^2}} \cdots dy\,dx \end{gather*}
We have determined all the limits on the iterated integral. Putting the bottom/top limits together with the shadow limits, the ice cream cone can be described by the inequalities \begin{gather*} -1/\sqrt{2} \le x \le 1/\sqrt{2}\\ -\sqrt{1/2 - x^2} \le y \le \sqrt{1/2 - x^2}\\ \sqrt{x^2+y^2} \le z \le \sqrt{1-x^2-y^2} \end{gather*} and the integral of the function $f(x,y,z)$ over $\dlv$ is \begin{align} \iiint_\dlv f\, dV = \int_{-1/\sqrt{2}}^{1/\sqrt{2}} \int_{-\sqrt{1/2-x^2}}^{\sqrt{1/2-x^2}} \int_{\sqrt{x^2+y^2}}^{\sqrt{1-x^2-y^2}} f(x,y,z) dz\,dy\,dx. \label{icecreamintegral} \end{align}
Example 3b
Find the volume of the ice cream cone of Example 3a..
Solution: Simply set $f(x,y,z)=1$ in equation \eqref{icecreamintegral}.
The volume of the ice cream cone $\dlv$ given by the integral \begin{align*} \iiint_\dlv dV = \int_{-1/\sqrt{2}}^{1/\sqrt{2}} \int_{-\sqrt{1/2-x^2}}^{\sqrt{1/2-x^2}} \int_{\sqrt{x^2+y^2}}^{\sqrt{1-x^2-y^2}} dz\,dy\,dx. \end{align*} We won't attempt to evaluate this integral in rectangular coordinates. Once you've learned how to change variables in triple integrals, you can read how to compute the integral using spherical coordinates.
Example 4
Find volume of the tetrahedron bounded by the coordinate planes and the plane through $(2,0,0)$, $(0,3,0)$, and $(0,0,1)$.

Applet loading
A tetrahedron. The tetrahedron is bounded by the coordinate planes ($x=0$, $y=0$, and $z=0$) and the plane through the three points (2,0,0), (0,3,0), and (0,0,1).
Solution: We know the equation for three of the surfaces of the tetrahedron, as they are the equations for the coordinates planes: $x=0$, $y=0$, and $z=0$. As an initial step, we can find the equation for the angled plane. You can follow the procedure in the second forming plane example to calculate that the plane is given by the equation \begin{align} 3x + 2y + 6z = 6. \label{plane_equation} \end{align}
To find the limits of the tetrahedron, we'll use the shadow method again, but this time, we'll think of the $y$-axis as being the vertical axis. You can imagine the sun that is casting the shadow as being at some point far on the positive $y$-axis.
With this orientation, the shadow of the tetrahedron is the maximal range of $x$ and $z$ over the tetrahedron. Since the tetrahedron gets wider in the $x$ and $z$ directions as $y$ decreases, the shadow of the tetrahedron is exactly the base of the tetrahedron in the $xz$-plane (the plane $y=0$), which is the triangle pictured below.
We approach the integral over this shadow as a double integral. In this shadow (and consequently in the tetrahedron itself), the total range of $z$ is \begin{align*} 0 \le z \le 1. \end{align*} To find the range of $x$ for each value of $z$, you can calculate from the figure of the shadow that the upper limit of $x$ is the line $z=1-x/2$ or $x=2(1-z)$. Given that the lower limit on $x$ is zero, the range of $x$ in the shadow for a given $z$ is \begin{align*} 0 \le x \le 2(1 - z). \end{align*} Alternatively, you could see that the upper limit on $x$ corresponds to the plane given by equation \eqref{plane_equation} when $y=0$. Plugging $y=0$ into equation \eqref{plane_equation} yields $3x + 6z=6$ or $x = 2(1-z)$.
For each value of $x$ and $z$ in the shadow, we need to integrate $y$ from the bottom to the top (viewing $y$ as the vertical axis). The bottom from this perspective is in the plane $y=0$, and the top is the angled plane of equation \eqref{plane_equation}, which we can solve for $y$ to write as $y=3(1-x/2 -z)$. Hence, for a given $z$ and $x$, the range of $y$ is \begin{align*} 0 \le y \le 3\left(1 - \frac{x}{2} - z\right). \end{align*}
To find the volume, we integrate the function 1 over this region: \begin{align*} &\int_0^1 \int_0^{2(1-z)} \int_0^{3(1- x/2 - z)} dy \, dx \, dz\\ &\qquad = \int_0^1 \int_0^{2(1-z)} 3\left(1 - \frac{x}{2} - z \right) dx \, dz\\ &\qquad = \int_0^1 3\left.\left[x - \frac{x^2}{4} -zx\right]_{x=0}^{x=2(1-z)}\right. dz\\ &\qquad = \int_0^1 3\left(2(1-z) - (1-z)^2 - 2z(1-z)\right) dz\\ &\qquad = \int_0^1 3(1 - 2z +z^2) dz\\ &\qquad = 3 \left.\left[ z - z^2 + \frac{z^3}{3} \right]_0^1\right.\\ &\qquad = 3\left(1 - 1 +\frac{1}{3}\right) = 3\left(\frac{1}{3}\right) = 1. \end{align*}
Example 5
Change the order of $x$ and $y$ in the integral we derived above, \begin{align*} \int_0^1 \int_0^{2(1-z)} \int_0^{3(1- x/2 - z)} dy \, dx \, dz, \end{align*} so that the order will be $dx \, dy \, dz$.
Solution: One way to change the order of integration is to build up the graph of the tetrahedron from the limits of the integral, and then repeat the procedure of Example 4 but let the shadow be cast from the positive $x$-axis. Instead, we'll illustrate an alternative procedure of calculating the new limits directly from the inequalities of the old limits.
If $y$ will be middle integral, we need limits of $y$ in terms of $z$ (independent of $x$).
For given $z$, how large can $y$ range? From the above limits, we know \begin{align*} 0 \le y \le 3\left(1 - \frac{x}{2} - z\right). \end{align*} The range is largest when $x=0$, so \begin{align*} 0 \le y \le 3\left(1 - z\right) \end{align*}
Then, given $z$ and $y$, we need to know the range of the $x$. The following relationship must still be true: \begin{align*} y \le 3\left(1 - \frac{x}{2} - z\right). \end{align*} We can rewrite this relationship in terms of $x$ as \begin{align*} \frac{3x}{2} \le 3 - 3z -y, \end{align*} or \begin{align*} x \le 2\left(1 - z - \frac{y}{3}\right). \end{align*}
Since we also know $x \ge 0$, the new limits of integration are \begin{align*} \int_0^1\int_0^{3(1-z)} \int_0^{2(1-z-y/3)} dx\, dy \, dz. \end{align*}
More examples
More examples of calculating triple integrals can be found in the pages describing the shadow method and cross section method of determining integration bounds.
Thread navigation
Multivariable calculus
- Previous: The cross section method for determining triple integral bounds
- Next: Introduction to changing variables in double integrals
Math 2374
Notation systems
Similar pages
- Introduction to triple integrals
- Triple integral change of variables story
- The shadow method for determining triple integral bounds
- The cross section method for determining triple integral bounds
- Introduction to changing variables in triple integrals
- Volume calculation for changing variables in triple integrals
- Examples of changing the order of integration in double integrals
- Double integrals where one integration order is easier
- Area calculation for changing variables in double integrals
- Triple integral change of variable examples
- More similar pages