Introduction to triple integrals
Remember how double integrals can be written as iterated integrals. Triple integrals are essentially the same thing as double integrals. (We just add a third dimension.) We will turn triple integrals into (triple) iterated integrals.
Just as with double integrals, the only trick is determining the limits on the iterated integrals. (Unfortunately, it's harder to draw in three dimensions.)
Before discussing how to set up the iterated integrals, we first address how to define triple integrals in the same way we define most of our integrals: with a Riemann sum.
Defined by Riemann sums
Let $f(x,y,z)$ be the density of a three-dimensional solid $\dlv$ at the point $(x,y,z)$ inside the solid. We want to define the triple integral of $f$ over $\dlv$ to be the total mass of $\dlv$.
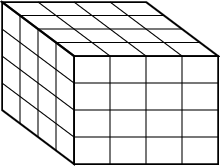
As with double integrals, we define the integral with Riemann sums. We chop up the solid $\dlv$ into small boxes, say with dimensions $\Delta x$, $\Delta y$, $\Delta z$. If $\dlv$ happened to be a cube, this chopping might look something like this.
The volume of each small box is \begin{align*} \Delta V = \Delta x \Delta y \Delta z. \end{align*}
Think of the boxes as being arranged in layers, with each layer arranged into rows and columns. We can then index the boxes so that box $ijk$ refers to the box in the $i$th row, the $j$th column, and the $k$th layer.
For each box, we pick a point in the box to represent that box. For box $ijk$, we call that point $(x_{ijk}, y_{ijk}, z_{ijk})$. Pretend that the density of box $ijk$ is constant, i.e., that the density is $f(x_{ijk}, y_{ijk}, z_{ijk})$ everywhere in that box. The mass of box $ijk$ is its density times it volume: \begin{align*} f(x_{ijk}, y_{ijk}, z_{ijk}) \Delta V. \end{align*}
We sum up these approximate masses to estimate the total mass of the solid $\dlv$. We obtain the Riemann sum \begin{align*} \sum_{ijk} f(x_{ijk}, y_{ijk}, z_{ijk})\Delta V, \end{align*} where the sum is over all small boxes.
Let $\Delta x \to 0$, $\Delta y \to 0$, and $\Delta z \to 0$ (and let the number of small boxes go to infinity). The Riemann sum approaches the triple integral over the solid $\dlv$, \begin{align*} \iiint_\dlv f\, dV = \lim_{\Delta x, \Delta y, \Delta z \to 0} \sum_{ijk} f(x_{ijk}, y_{ijk}, z_{ijk}) \Delta V, \end{align*} assuming $f$ is continuous. The triple integral is the actual mass of $\dlv$.
Triple iterated integrals
If the solid $\dlv$ is a cube defined by $a \le x \le b$, $c \le y \le d$, and $p \le z \le q$, then we can easily write the triple integral as an iterated integral. We could first integrate $x$ from $a$ to $b$, then integrate $y$ from $c$ to $d$, and finally integrate $z$ from $p$ to $q$, \begin{align*} \iiint_\dlv f\, dV = \int_p^q \left(\int_c^d \left(\int_a^b f(x,y,z) dx \right ) dy \right) dz. \end{align*} This order of integration corresponds a certain way of ordering the terms in the Riemann sum: first, we sum over rows $i$, then we sum over columns $j$, and finally we sum over layers $k$.
Just as with double integrals, other orders of integration are possible. We could, for example, first integrate with respect to $z$, then integrate with respect to $x$, and lastly integrate with respect to $y$, \begin{align*} \iiint_\dlv f\, dV = \int_c^d \left(\int_a^b \left(\int_p^q f(x,y,z) dz \right ) dx \right) dy \end{align*}
The integration always proceeds from the inside to the outside. The integration order coincides with the order that the differentials (e.g. $dx$) appear, so we can specify the integration order by a list of the differentials. The previous integral is in the order $dz\,dx\,dy$. With this understanding, the parentheses become optional, and we usually omit them, writing the previous integral as \begin{align*} \iiint_\dlv f\, dV = \int_c^d \int_a^b \int_p^q f(x,y,z) dz\, dx \, dy. \end{align*}
The iterated integral is simple when the solid $\dlv$ is a rectangular solid (like a cube, but where all edges aren't necessarily the same length). For more complicated shapes, finding the limits of integration can be tricky.
As a first step, just remember these rules, which are analogous to the rules we had for limits on double iterated integrals.
- The outer limits have to be constant. They cannot depend on any of the variables.
- The middle limits can depend on the variable from the outer integral only. They cannot depend on the variable from the inner integral.
- The inner limits can depend on the variable from the outer integral and the variable from the middle integral.
For example, the following integral makes sense \begin{align*} \iiint_\dlv f\, dV = \int_2^3 \int_{1-z}^0 \int_{-y^2-z^2}^{y^2+z^2} f(x,y,z) dx\, dy \, dz. \end{align*} It describes the integral of $f$ over the region $\dlv$ defined by \begin{gather*} 2 \le z \le 3,\\ 1-z \le y \le 0,\\ -y^2-z^2 \le x \le y^2+z^2 \end{gather*} (not that you should be able to visualize what $\dlv$ looks like).
The following integral does not make sense \begin{align*} \iiint_\dlv f\, dV = \color{red}{\xcancel{\color{black}{\int_y^x \int_{1}^{2x} \int_0^1 f(x,y,z) dx \, dy \, dz.}}} \end{align*} Can you see why? The outer integral limits depend on both $x$ and $y$ (but $y$ isn't defined until you go inside the middle integral, and $x$ isn't defined until you go inside the inner integral). Also, the middle integral limits depend on $x$.
A tricky part of triple integrals is determining the limits of integration (or bounds). Two methods for determining bounds are the shadow method and the cross section method. Nothing beats practice in learning to compute triple integrals, and you can try your hand on some of these triple integral examples.
Thread navigation
Multivariable calculus
- Previous: Double integrals where one integration order is easier
- Next: The shadow method for determining triple integral bounds
Math 2374
Notation systems
Similar pages
- Triple integral examples
- Triple integral change of variables story
- The shadow method for determining triple integral bounds
- The cross section method for determining triple integral bounds
- Introduction to changing variables in triple integrals
- Volume calculation for changing variables in triple integrals
- Area calculation for changing variables in double integrals
- Triple integral change of variable examples
- The integrals of multivariable calculus
- Illustrated example of changing variables in double integrals
- More similar pages