Math Insight

Introduction to changing variables in triple integrals

Changing variables in triple integrals is a lot like changing variables in double integrals. The basic concepts are the same, only we have to worry about the additional third dimension. For a good review of the necessary steps for changing variables put into the context of triple integrals, we recommend you read the triple integral change variables story. The page gives a more traditional perspective on the process.

An example to motivate the problem

Imagine you need to calculate the mass of dome in the shape of a half a spherical shell with inner radius of 3 meters and outer radius of 5 meters, as pictured below. If we center our $(x,y,z)$ coordinates at in the middle of the bottom of the dome, then the density of the dome at the point $(x,y,z)$ is $f(x,y,z) = 5+z$, where $f$ is in units of kilograms per cubic meter. The mass of the dome is the integral of the density $f$ over the region describing the dome.

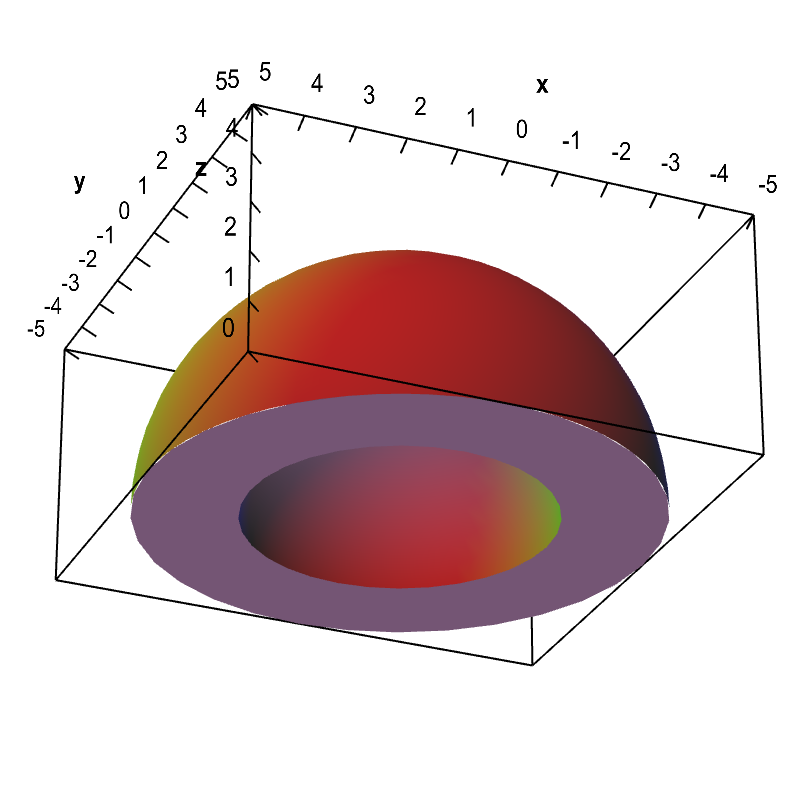
Applet loading

Let $\dlv$ be the region of the dome. Then we can write its mass as the triple integral \begin{gather*} \text{mass} = \iiint_{\dlv} f(x,y,z) dV. \end{gather*} Given the above description, we can describe the dome $\dlv$ as the region \begin{gather*} 9 \le x^2+y^2+z^2 \le 25\\ z \ge 0. \end{gather*}

To turn the intergral into an iterated integral over $x$, $y$, and $z$, we need to determine the integration bounds for each variable. Let's try to do this for the integration order $dx\,dy\,dz$. Then, the bounds on $z$ are simple, as it is the outer integration variable. We just need the total range of $z$ over the dome. Letting $z$ range from the top of the dome to its bottom, we get the interval \begin{gather*} 0 \le z \le 5. \end{gather*}

If we try to use the cross section method to determine the bounds on $x$ and $y$, then for each value of $z$, we need to let $x$ and $y$ range over the cross section of the dome at the height of $z$. In other words, we need $x$ and $y$ to be determined by \begin{gather*} 9-z^2 \le x^2+y^2 \le 25-z^2 \end{gather*} where we view $z$ as a constant. If $z < 3$, then $x$ and $y$ must range over an annulus (or a ring), such as the cross section for $z=0$, which is the bottom of the dome viewable in the above picture. For $z > 3$, the cross section is a circle. It will get very messing to come up with appropriate bounds for $\dlv$ in this fashon.

Simplifying by changing variables

The dome problem illustrates one reason why we may want to change variables: to find an simpler region $\dlv^*$ over which to calculate the integral. For the dome example, the description of the dome will be much easier if we use spherical coordinates instead of the Cartesian coordinates we used above. In terms of the spherical coordinates $\rho$, $\theta$, and $\phi$, the description of the dome is simple. The radius $\rho$ ranges in the interval $3 \le \rho \le 5$. The angle $\pi$ ranges over its entire range $0 \le \theta \le 2\pi$. Since we have only the top half of the sphere, the angle $\phi$ ranges only over half its range, i.e., $0 \le \phi \le \pi/2$.

These bounds on the spherical coordinates determine the region $\dlv^*$ in $\rho\theta\phi$-space. In this space, the dome actually looks like a rectangular box, as all the limits of the region \begin{gather} 3 \le \rho \le 5\notag\\ 0 \le \theta \le 2\pi\label{domespherical}\\ 0 \le \phi \le \pi/2\notag \end{gather} are constant, independent of the other variables.

The relation between spherical and Cartesian coordinates can be written as a mapping: \begin{gather} (x,y,z) = \cvarf(\rho,\theta,\phi) = ( \rho\sin\phi\cos\theta, \rho\sin\phi\sin\theta, \rho\cos\phi). \label{sphericaltrans} \end{gather} As $(\rho,\theta,\phi)$ ranges over the box $\dlv^*$ in spherical coordinates space, the point $(x,y,z) = \cvarf(\rho,\theta,\phi)$ ranges over the dome $\dlv$, as illustrated in the below applet. The process of changing variables transforms the integral in terms of the variables $(x,y,z)$ over the dome $\dlv$ to an integral in terms of the variables $(\rho, \theta, \phi)$ over the region $\dlv^*$.

Since the function $f(x,y,z)$ is defined in terms of $(x,y,z)$, we cannot simply integrate $f$ over the box $\dlv^*$. Instead, we must first compose $f$ with the change of variables function $\cvarf$. As we integrate the composition of functions $f(\cvarf(\rho,\theta,\phi))$ over $\dlv^*$, we add up the density calculated at the points $(x,y,z) = \cvarf(\rho,\theta,\phi)$ of the dome $\dlv$.

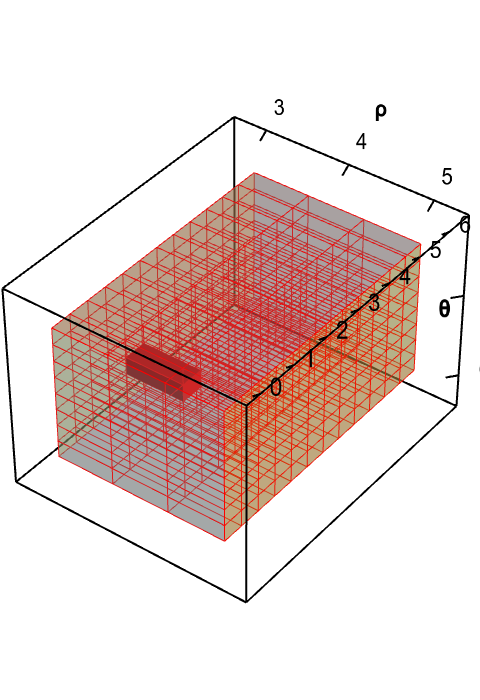
Applet loading

Applet loading

A change of variables for a dome-shaped domain changes volume. The change of variables $\cvarf$ from spherical to Cartesian coordinates maps the rectangular solid $\dlv^*$ (first panel, in red) onto a dome $\dlv$ (second panel, in blue). A point $(\rho,\theta,\phi)$ in $\dlv^*$ in mapped to a point $(x,yz)=\cvarf(\rho,\theta,\phi)$ in $\dlv$. If one chops up $\dlv^*$ into small boxes, the function $\cvarf$ maps the small boxes of $\dlv^*$ onto curvy regions of different size in $\dlv$. You can explore the mapping by dragging the red box $\dlv^*$ or the blue region in $\dlv$. The region in the other panel moves according to the map. The volume of the blue region varies with the position, illustrating how the map $\cvarf$ stretches the region $\dlv^*$ by different amounts depending on the location.

More information about applet.

The last step is to correctly account for the volume element $dV$. In the original Cartesian coordinates $(x,y,z)$, the volume element was simply $dV = dx\,dy\,dz$. The temptation may be to use the analogous expression $d\rho\,d\theta\,d\phi$ for the volume element, but that element measures volume in the box $\dlv^*$ (illustrated by the small red boxes the above applet) not volume in the dome $\dlv$ (illustrated by the small blue curvy regions). The fact that the small blue regions have different volume than the small red regions shows that $\cvarf$ changes volume as it transforms spherical coordinates to Cartesian coordinates.

To calculate the volume transformation, one can approximate the curvy blue regions as parallelepipeds. Then, one can easily calculate their volume using the scalar triple product. One can calculate that these parallelepipeds are spanned by vectors proportional to the partial derivatives of the change of variables function $\cvarf$, so that their volume is proportional to the scalar triple product of these partial derivatives.

The end result is that rather than using $d\rho\,d\theta\,d\phi$ for the volume element, we must use \begin{align*} dV=\left| \pdiff{\cvarf}{\rho} \cdot \left(\pdiff{\cvarf}{\theta} \times \pdiff{\cvarf}{\phi}\right)\right|d\rho\,d\theta\,d\phi= | \det \jacm{\cvarf}|\,d\rho\,d\theta\,d\phi, \end{align*} where $\jacm{\cvarf}$ is the matrix of partial derivatives of $\cvarf$. See this page for more of the details in this calculation.

We can think of the expression $| \det \jacm{\cvarf}|$ as the volume expansion factor, as it captures how $\cvarf$ stretches or shrinks $\dlv^*$ as it maps it into $\dlv$.

Putting the steps together, we can write the change of variables into spherical coordinates as \begin{align*} \iiint_\dlv f(x,y,z) dV = \iiint_{\dlv^*} f(\cvarf(\rho,\theta,\phi)) \left|\det\jacm{\cvarf}(\rho,\theta,\phi)\right| d\rho\,d\theta\,d\phi. \end{align*} For the spherical coordinate change of variables function \eqref{sphericaltrans}, the volume expansion factor is $|\det\jacm{\cvarf}(\rho,\theta,\phi)|=\rho^2\sin\phi$, as shown on the example page. Since the density is $f(x,y,z) = 5+z$, composing the function with the change of variable transformation yields \begin{gather*} f(\cvarf(\rho,\theta,\phi)) = f( \rho\sin\phi\cos\theta, \rho\sin\phi\sin\theta, \rho\cos\phi) = 5+ \rho\cos\phi. \end{gather*} Given that the dome in spherical coordinates is given by the inequalities \eqref{domespherical}, we can rewrite the integral for the dome mass as \begin{align*} \text{mass} &= \iiint_{\dlv} f(x,y,z) dV\\ &= \int_3^5 \int_0^{2\pi}\int_0^{\pi/2} (5+ \rho\cos\phi)\rho \,\sin^2\phi \, d\phi\,d\theta\,d\rho. \end{align*} Although it still takes some trignometric identities and a bit of work, it's a lot easier to calculate that the mass is $1388\pi/3$ kilograms after changing variables to spherical coordinates than it would be if you stayed with Cartesian coordinates.

In general, we tend to write a triple integral change of variables as $\cvarf(\cvarfv,\cvarsv,\cvartv)$, in which case the change of variables formula looks like \begin{align*} \iiint_\dlv f(x,y,z) \, dV = \iiint_{\dlv^*} f(\cvarf(\cvarfv,\cvarsv,\cvartv)) \left| \det \jacm{\cvarf}(\cvarfv,\cvarsv,\cvartv)\right| \,d\cvarfv\,d\cvarsv\,d\cvartv. \end{align*} As with double integrals, we can also denote the expansion factor using partial derivative notation, denoting the volume expansion factor as \begin{gather*} \left| \det \jacm{\cvarf}(\cvarfv,\cvarsv,\cvartv)\right| = \left|\pdiff{(x,y,z)}{(\cvarfv,\cvarsv,\cvartv)}\right| \end{gather*} and the change of variables formula as \begin{align*} \iiint_\dlv f(x,y,z) \, dV = \iiint_{\dlv^*} f(\cvarf(\cvarfv,\cvarsv,\cvartv)) \left|\pdiff{(x,y,z)}{(\cvarfv,\cvarsv,\cvartv)}\right| \,d\cvarfv\,d\cvarsv\,d\cvartv. \end{align*}

We've clearly skipped over a lot of details in this introduction. To fill in the missing parts, you can read how we obtained the volume expansion factor. To help you tie all the steps together, you can peruse a story outlining the steps. You can also read examples of changing variables into spherical and cylindrical coordinates.