Math Insight

Triple integral change of variable examples

Spherical coordinates example

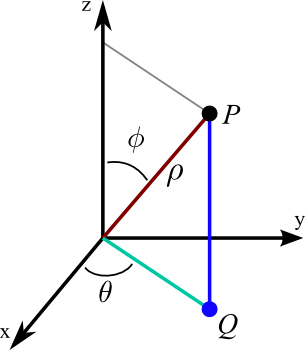
For spherical coordinates, the change of variables function is \begin{align*} (x,y,z) &= \cvarf(\rho,\theta,\phi) \end{align*} where the components of $\cvarf$ are given by \begin{align*} x &= \rho \sin\phi \cos\theta\\ y &= \rho \sin\phi \sin\theta\\ z &= \rho \cos\phi. \end{align*} We can compute that \begin{align*} \jacm{\cvarf}(\rho,\theta,\phi) &= \left| \begin{array}{ccc} \displaystyle \pdiff{x}{\rho} & \displaystyle \pdiff{x}{\theta} & \displaystyle \pdiff{x}{\phi}\\ \displaystyle \pdiff{y}{\rho} & \displaystyle \pdiff{y}{\theta} & \displaystyle \pdiff{y}{\phi}\\ \displaystyle \pdiff{z}{\rho} & \displaystyle \pdiff{z}{\theta} & \displaystyle \pdiff{z}{\phi}\\ \end{array} \right|\\ &= \left| \begin{array}{ccc} \sin\phi \cos\theta & - \rho\sin\phi \sin\theta & \rho\cos\phi\cos\theta\\ \sin\phi \sin\theta & \rho \sin\phi \cos\theta & \rho\cos\phi\sin\theta\\ \cos\phi & 0 & -\rho \sin\phi \end{array} \right|\\ &= -\rho^2 \sin\phi. \end{align*}

The change of variable factor is the absolute value of the determinant \begin{align*} \left| \jacm{\cvarf}(\rho,\theta,\phi) \right| = \rho^2 \sin\phi. \end{align*} This means that the map from spherical coordinates to rectangular coordinates changes volume by the factor $\rho^2 \sin\phi$. For this reason, you need to do the above calculation only once. Now, you can just remember that the factor for spherical coordinates is $\rho^2 \sin\phi$.

Now we're ready for the example: find the mass of a star $\dlv$ that is a ball of radius 3 centered at the origin if the density of the star is $g(x,y,z) = 10 - x^2-y^2-z^2$.

If we try to compute the integral directly in rectangular coordinates, it isn't so easy: \begin{align*} &\iiint_\dlv g(x,y,z) dx\,dy\,dz\\ &= \int_{-3}^3 \int_{-\sqrt{9-z^2}}^{\sqrt{9-z^2}} \int_{-\sqrt{9-z^2-y^2}}^{\sqrt{9-z^2-y^2}} (10 - x^2 -y^2-z^2) dx\,dy\,dz \end{align*} This would lead to a mess.

We can find the mass of the star more easily in spherical coordinates. The star density $g(x,y,z) = 10 - x^2-y^2-z^2$ becomes $g(\cvarf(\rho,\theta,\phi)) = 10-\rho^2$.

In spherical coordinates, the integral over ball of radius 3 is the integral over the region \begin{align*} 0 \le \rho \le 3, \quad 0 \le \theta \le 2\pi, \quad 0 \le \phi \le \pi. \end{align*} The volume element is $\rho^2 \sin\phi \,d\rho\,d\theta\,d\phi$.

Therefore, the mass of the star is \begin{align*} &\int_0^3 \int_0^{2\pi} \int_0^{\pi} (10-\rho^2) \rho^2 \sin\phi \,d\phi\,d\theta\,d\rho\\ &=\int_0^3 \int_0^{2\pi} \left.(10-\rho^2) \rho^2 (-\cos\phi ) \right|_{\phi=0}^{\phi=\pi} d\theta\,d\rho\\ &=\int_0^3 \int_0^{2\pi} (10-\rho^2) \rho^2 2 d\theta\,d\rho\\ &=\int_0^3 4\pi (10-\rho^2) \rho^2 d\rho = \frac{828 \pi}{5} \approx 520. \end{align*}

Cylindrical coordinates example

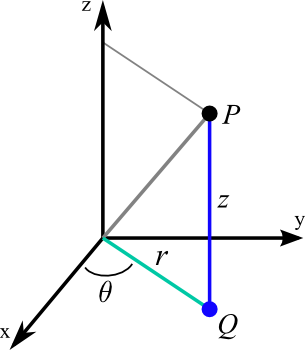
For cylindrical coordinates, the change of variables function is \begin{align*} (x,y,z) &= \cvarf(r,\theta,z) \end{align*} where the components of $\cvarf$ are given by \begin{align*} x &= r \cos\theta\\ y &= r \sin\theta\\ z &= z. \end{align*} We can compute that \begin{align*} \jacm{\cvarf}(\rho,\theta,\phi) &= \left| \begin{array}{ccc} \displaystyle \pdiff{x}{r} & \displaystyle \pdiff{x}{\theta} & \displaystyle \pdiff{x}{z}\\ \displaystyle \pdiff{y}{r} & \displaystyle \pdiff{y}{\theta} & \displaystyle \pdiff{y}{z}\\ \displaystyle \pdiff{z}{r} & \displaystyle \pdiff{z}{\theta} & \displaystyle \pdiff{z}{z}\\ \end{array} \right|\\ &= \left| \begin{array}{ccc} \cos\theta & -r\sin\theta &0\\ \sin\theta & r \cos\theta &0\\ 0 & 0 & 1 \end{array} \right|\\ &= r \cos^2\theta + r\sin^2\theta = r. \end{align*} Volume changes by $|r|=r$ (just like area change for polar coordinates). Replace $dx\,dy\,dz$ by $r \,dr\,d\theta\,dz$.

We can calculate the following example problem. Find the volume of cone of height 1 and radius one. It is bounded by surface $z=\sqrt{x^2+y^2}$ and plane $z=1$.

The volume is \begin{align*} \int_{-1}^{1} \int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \int_{\sqrt{x^2+y^2}}^{1} dz \, dy\, dz. \end{align*}

The integral is easier to compute in cylindrical coordinates. In cylindrical coordinates, the cone is described by \begin{align*} 0 \le \theta \le 2\pi, \quad 0 \le r \le 1,\quad r \le z \le 1. \end{align*}

The volume of cone is \begin{align*} &\int_0^1 \int_0^{2\pi} \int_r^{1} r \, dz\,d\theta\,dr\\ &=\int_0^1 \int_0^{2\pi} (1 -r)r\, d\theta\,dr\\ &=\int_0^1 2\pi (1-r)r\, dr = \frac{\pi}{3}. \end{align*}

Ice cream cone revisited

Armed with the knowledge of how to change to spherical coordinates, we can now revisit the ice cream cone example.

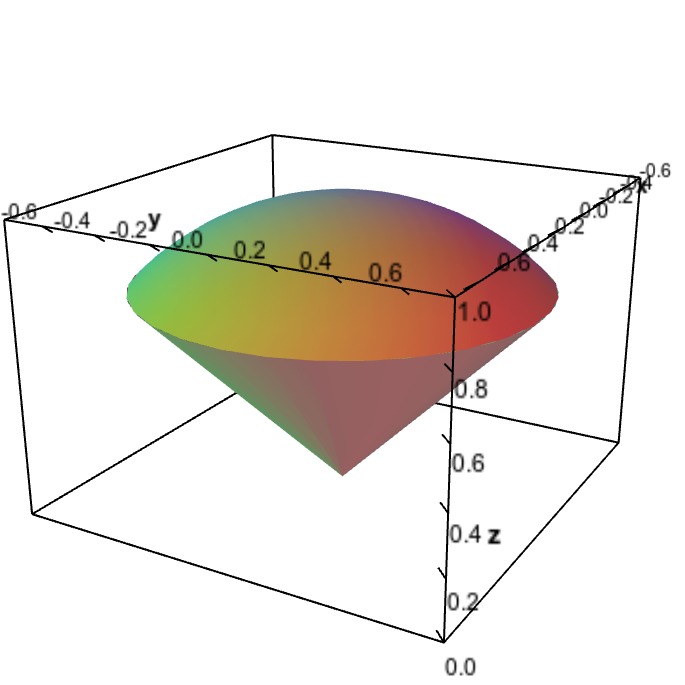
Applet loading

Ice cream cone region. The ice cream cone region is bounded above by the half-sphere $z=\sqrt{1-x^2-y^2}$ and bounded below by the cone $z=\sqrt{x^2+y^2}$.

More information about applet.

On the triple integral examples page, we tried to find the volume of an ice cream cone $\dlv$ and discovered the volume was \begin{align*} \iiint_\dlv dV = \int_{-1/\sqrt{2}}^{1/\sqrt{2}} \int_{-\sqrt{1/2-x^2}}^{\sqrt{1/2-x^2}} \int_{\sqrt{x^2+y^2}}^{\sqrt{1-x^2-y^2}} dz\,dy\,dx. \end{align*}

We need to describe the bounds in terms of spherical coordinates. Since the cone is symmetrical around the $z$ axis, $\theta$ is easy. $0 \le \theta \le 2\pi$ in the cone and the ranges of the other variables don't depend on $\theta$. Also, we see that $0 \le r \le 1$, since a given line from the origin extends until it hits the sphere $z=\sqrt{1-x^2-y^2}$, which is a sphere of radius 1. Lastly, $\phi$ is determined by requiring that we are in the cone $z \ge \sqrt{x^2+y^2}$. (To see this is exactly a condition on $\phi$, look at the page on spherical coordinates.) On the cone, $z=\sqrt{x^2+y^2}$, $\phi = \pi/4$. Consquently, the condition on $\phi$ is $0 \le \phi \le \pi/4$.

In summary, the ice cream cone is described by \begin{align*} 0 \le \theta \le 2\pi, \quad 0 \le r \le 1, \quad 0 \le \phi \le \pi/4. \end{align*}

Changing to spherical coordinates, we calculate that the volume of the ice cream cone is \begin{align*} \int_0^1 \int_0^{2\pi} \int_0^{\pi/4} \rho^2 \sin \phi d\phi \,d\theta\,d\rho &=\int_0^1 \int_0^{2\pi} [\cos(0)-\cos(\pi/4)] \rho^2 d\theta\,d\rho\\ &=\int_0^1 \int_0^{2\pi} \frac{2-\sqrt{2}}{2} \rho^2 d\theta\,d\rho\\ &=\int_0^1 \pi (2-\sqrt{2}) \rho^2 d\rho\\ &= \pi \frac{2-\sqrt{2}}{3}. \end{align*}