Highlighted pages
- The idea behind Stokes' theorem
Introduction to Stokes' theorem, based on the intuition of microscopic and macroscopic circulation of a vector field and illustrated by interactive graphics. - Parametrization of a line
Introduction to how one can parametrize a line. Interactive graphics illustrate basic concepts. - An introduction to the directional derivative and the gradient
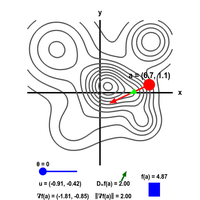
Interactive graphics about a mountain range illustrate the concepts behind the directional derivative and the gradient of scalar-valued functions of two variables. - The components of the curl
Illustration of the meaning behind the components of the curl. - Forming planes
A description of ways to specify a plane. Interactive graphics illustrate the concepts.
Recent pages
- A birth-death process
Added April 13, 2022 - A stochastic process introduction
Added April 13, 2022 - An introduction to neural coding and decoding
Added April 3, 2022 - More new items
Highlighted applets
The gradient and directional derivative are illustrated by a level curve plot of a mountain range. The applet interactively computes the gradient and the directional derivative at different points and directions.
Illustration of a linear transformation mapping the unit cube to a parallelepiped while reversing orientation.
Welcome to Math Insight
The Math Insight web site is a collection of pages and applets designed to shed light on concepts underlying a few topics in mathematics. The focus is on qualitative description rather than getting all technical details precise. Many of the pages were designed to be read even before students attend lecture on the topic, so they are intended to be somewhat readable introductions to the basic ideas.
You can browse the pages organized into threads, which are sequences through a subset of pages organized by particular topics. An index can help you find pages discussing a particular term. You can also search through the pages, applets, and image captions. A few pages allow you to change the notation system used to render the mathematics.
We hope Math Insight can help you understand key mathematical concepts. We welcome comments on how we can improve it.