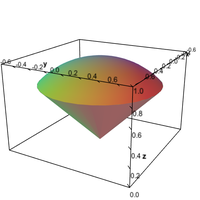List of applets
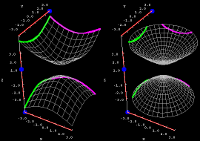
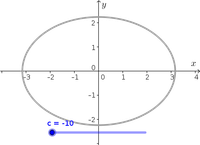
- Applet: Hyperboloid of two sheets cross sections (Interactive)
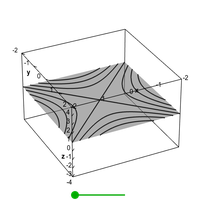
Illustration of the vertical and horizontal cross sections of a hyperboloid of two sheets plotted with both square and circular domains. - Applet: Ice cream cone region
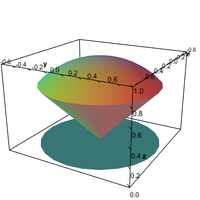
An ice cream cone shaped region used for the domain of triple integrals. - Applet: Ice cream cone region with shadow
An ice cream cone shaped region used for the domain of triple integrals, with shadow. - Applet: A spherical implicit surface
The graph of the equation $x^2+y^2+z^2=1$ is the unit sphere centered at the origin. - Applet: Indefinite integral of a function (Interactive)
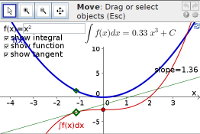
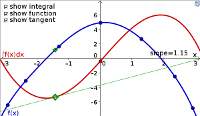
Illustration of the indefinite integral of a function, showing the relationship between the integral's tangent line and the function itself. - Applet: Indefinite integral of interpolating polynomial (Interactive)
Illustration of the relationship between a polynomial and its indefinite integral. - Applet: Integrate constant velocity (Animation, Interactive)
- Applet: Idea of integration using oscillating velocity
- Applet: The Kuramoto order parameters (Interactive)
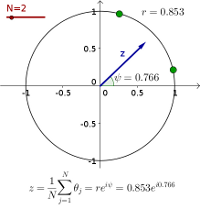
Illustration of how the Kuramoto order parameters capture the degree of synchrony among a collection of phase oscillators. - Applet: Level curves of an elliptic paraboloid shown with graph (Interactive)
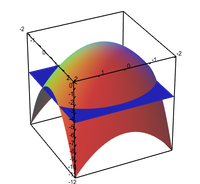
The level curves of an elliptic paraboloid are shown as the intersection of a horizontal plane with the graph. - Applet: Level curves of a hyperbolic paraboloid (Interactive)
A level curve plot of the function $f(x,y)=x^2-y^2$ that can be transformed into the graph of the function. - Applet: A level curve of an elliptic paraboloid
An illustration of a level curve of the function $f(x,y) = -x^2-2y^2$. - Applet: Level surface of a function of three variables (Interactive)
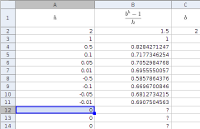
An illustration of a level curve of the function $f(x,y,z) = 10 e^{-9x^2-4y^2-z^2}$. - Applet: Limit of b to the h minus one over h as h tends to zero (Interactive)
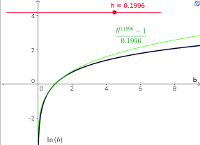
One can calculate values of an expression for smaller and smaller values of h in order to estimate the limit as h tends to zero. - Applet: Limit of b to the h minus one over h as h tends to zero converges to the natural logarithm (Interactive)
Demonstration that a function involving an exponential approaches the natural logarithm in the limit that a parameter h goes to zero. - Applet: Linear vector field
- Applet: Linear vector field with nullclines
- Applet: Linear 2d flow: growth and decay
- Applet: Linear 2d flow: oscillatory growth and decay
- Applet: Linear 2d flow: pure oscillation
« Previous
| Page 9 of 18 |
Next »