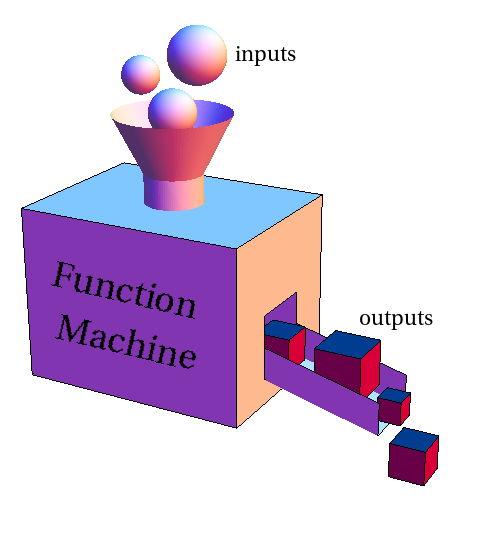
The function machine

The technical definition of a function

The following technical definition of a function is a little abstract.

Given a set of inputs $X$ and a set of possible outputs $Y$, a function is relation between these sets, i.e., a collection of ordered pairs of the form $(x,y)$ where $x \in X$ and $y \in Y$ (confused?), that satisfies one condition: every element $x$ in the domain $X$ must be paired with exactly one element $y$ in the codomain $Y$.

That's it. A function $f$ is just this collection of ordered pairs. Since we know each element $x \in X$ is paired with exactly one element $y \in Y$, we could denote this element by $y=f(x)$ so that the ordered pairs are denoted by $(x,f(x))$.

You may not find this set-of-ordered-pairs definition extremely illuminating. But, that's OK, as there are other ways to explain the concept of a function that may be more helpful at first. One tool for understanding functions is the function machine metaphor. Once you understand the concepts of functions better, you can always go back and try unpacking the technical definition of a function. You never know; you may end up appreciating the definition in the end.

The function machine metaphor

We can view a function as something that can take an object (as long as the object is in its domain) and turn it into (or map it to) a different object. We can imagine it is some machine that does this transformation. You put some object into its input funnel. If the input object fits into the funnel, then the function machine will process that object and turn it into some other object, which comes out its output chute.

In this illustration, the inputs are spheres of various sizes (the domain presumably contains only those spheres that are small enough to fit into the funnel). The outputs are illustrated by the cubes coming out of the chute. Hence, this function transforms each sphere into a cube.

We may usually think of functions as taking numbers for inputs and spitting out numbers as outputs, but there's no need to take such a limited view of functions. There's nothing about a function machine that implies it must deal with numbers. Any collection of objects could serve as the domain or codomain, as we illustrate with examples.

The power of the function machine metaphor

The function machine metaphor is quite versatile and powerful. It can be used to explain many important properties of functions and concepts involving functions.

The domain: The domain is simply the set of objects that fit into the input funnel and can be processed by the function machine.
The codomain: You could think of the codomain as the set of objects that could theoretically fit out the chute.
The range: The range is the set of objects that would come out the chute if you put all the elements of the domain into the funnel.
The unique pairing: If the machine is in good condition, it should always produce an output when you put in an input. If you put in the same input multiple times, the machine should always yield the same output. In this way, each element of the domain is paired with exactly one output from the codomain.
Parameters: Parameters of a function can be viewed as dials that change the behavior of the function machine.
Composition: One can use multiple function machines to illustrate the composition of functions.
Inverse: The inverse of a function is equivalent to running the machine backwards. But, if two different input elements are transformed into the same output element, the backward function machine won't know which of the input elements to spit out and the inverse isn't defined.

Of course, the function machine metaphor isn't perfect. A function doesn't actually destroy its inputs and turn them into its outputs. That's good when we define the mother function, so we don't actually turn people into their mothers.

To further explore the idea of a function, you can read some examples.

Math Insight