Math Insight

Function machine parameters

The function machine is a handy metaphor that illustrates how functions work. A function $f$ takes an input, say represented by the variable $x$, and spits out the value $f(x)$.

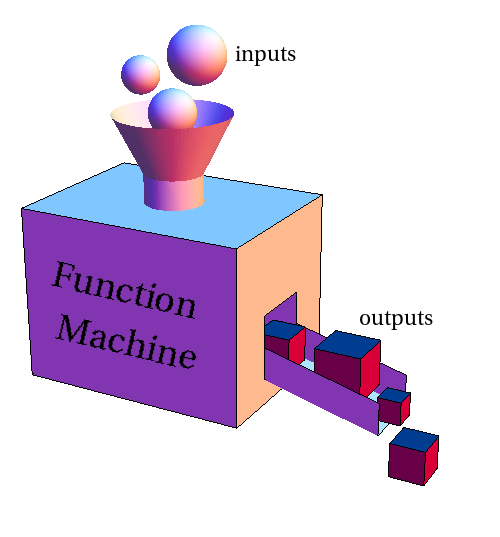
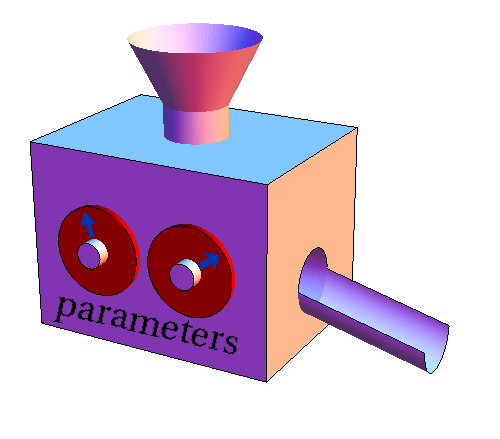
The function machine metaphor can also aid one in understanding how a function can depend on parameters. Parmameters are additional quantities that influence the behavior of the function. However, unlike the input variables, parameters are typically viewed as being held constant, or possibly changing slowly.

The influence of parameters on a function is the like influence of dials on a machine. For a given setting of the dials, the machine processes the inputs in a certain way. If one leaves the dials fixed, then the function machine always spits out the same output value for a given fixed input value.

If one wishes to change how the machine is operating, one can adjust one of the dials, i.e., change one of the parameters. When the dials are changed, the machine still process the inputs and turns them into outputs. However, with new parameters, for the same fixed input value, the function machine may now spit out a different output value than it did before the parameters were changed.

For example, we could define a quadratic function $f$ with three parameters $a$, $b$, and $c$ as \begin{align*} f(x) = ax^2 + bx +c. \end{align*} For a given set of parameters, such as $a=b=c=1$, the function $f$ behaves like a normal function. Since with these parameters, $f(x)=x^2+x+1$, whenever we put $x=2$ in the function machine, it always produces $f(2) = 2^2+2+1=7$.

When we change the parameters, we turn $f$ into a different function. For example, if we change $a$ into $a=2$, now $f$ operates using the formula $f(x) = 2x^2+x+1$, and $f(2)=2\cdot 2^2+2+1 =11$. In this sense, a function with parameters represents a whole family of functions, one for each value of the parameters.

If we don't know specific values for the parameter, we can still use the function machine to operate on input values. If we leave the parameters $a$, $b$, and $c$ as their symbols, then $f(2)= 4a+2b+c$. Then, once we know numerical values for the parameters, we can immediately determine a numeric value for $f(2)$.