Constructing a mathematical model for penicillin clearance
In developing a model of bacteria growth, we detailed every step of building the model from the data. Since we assumed the change in the population size in one time step was a linear function of the population size, the model was so simple that we could even solve it. We ended up with a fairly simple expression showing the exponential growth of the population size.
Here we'll examine a situation that seems completely different. We'll look at what happens when we give a patient a bolus injection (a one-time injection) of penicillin. In this case, of course, the penicillin won't start multiplying like bacteria in the patient. Instead, the body (i.e., the kidneys) will start removing the penicillin from the body. However, if we make a model where the amount of penicillin removed is a linear function of the amount penicillin in the blood, the model is starting to look a lot like the bacteria growth model. In fact, we'll get exponential decay of the amount of penicillin in the blood.
There's one more big difference between the bacteria growth example and this page. Here, we'll just get you started on the process, giving you background information about the drug clearance. We then let you go make the model on your own.
Background
When penicillin was first discovered, its usefulness was limited by the efficiency with which the kidney eliminates penicillin from the blood plasma (blood minus blood cells) passing through it. The modifications that have been made to penicillin (leading to amphicillin, moxicillin, mezlocillin, etc.) have enhanced its ability to cross membranes and reach targeted infections and reduced the rate at which the kidney clears the plasma of penicillin.
Even with these improvements in penicillin, the kidneys can still remove penicillin fairly rapidly. In this project, you will build a mathematical model of penicillin clearance based on an assumption of how the kidneys operate. The secret to your success will be to build into the model a key parameter that captures the speed of the penicillin clearance. Then, you can estimate the model parameter by fitting predictions of the model to data. Lastly, you will compare your model predictions to the data to see how well the model matches the data.
The assumption behind the model is that the amount of penicillin removed by the kidneys in a five minute interval is proportional to the total amount of penicillin. We can formulate this assumption as a word model for the renal (i.e., kidney) clearance of penicillin.
Renal clearance of penicillin
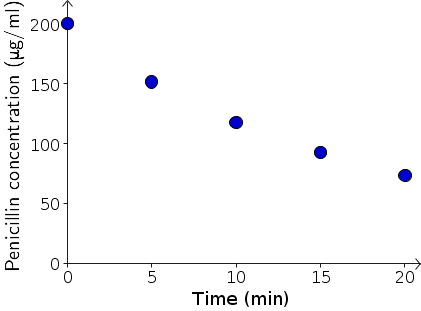
In each five minute interval following penicillin injection, the kidneys remove a fixed fraction of the penicillin that was in the plasma at the beginning of the five minute interval.
Your goal is to translate this word model into a mathematical model that has a parameter that determines how much penicillin the kidneys remove in each interval. You can then use the below data to determine this parameter.
The following table and graph contain data for serum penicillin concentrations at 5 minute intervals for the 20 minutes following a bolus injection (a one-time injection) of 2 g into the serum of “five healthy young volunteers” (read “medical students”) taken from T. Bergans, Penicillins, in Antibiotics and Chemotherapy, Vol 25, H. Schøonfeld, Ed., S. Karger, Basel, New York, 1978. We are interpreting serum in this case to be plasma.
Your turn
Now its your turn to develop a mathematical model of penicillin clearance. You can use a procedure similar to the one we used to developed the model of bacteria growth. Your model should be based on
- the above data, and
- the assumption that the drop in penicillin concentration each 5 minutes will depend linearly on the concentration.
If all goes well, you should be able to create a model that has an unknown parameter, fit the model to determine that parameter from the data, and then compare your model prediction to the data to see how well you did.
When you are all finished, you can compare your results to some findings from the research literature. Analysis of some numbers from the research literature seems to indicate that the all of the blood plasma of a human passes through the kidneys every 5 minutes and that the kidneys remove about 20% of the penicillin in the blood that passes through them.1 You should not use or assume 20% in your model. Instead, you create your model imagining that you never heard the 20% figure. After you are finished with your model, you can determine if your analysis of the above data yields a result close to that rate of clearance.
Instructions from writing up the penicillin project are here.
For more practice on building dynamical system models, try out the exercises.
Thread navigation
Elementary dynamical systems
- Previous: Bacteria growth model exercises
- Next: Penicillin clearance model exercises
Math 1241, Fall 2020
- Previous: Bacteria growth model exercises
- Next: Penicillin clearance model exercises
Math 201, Spring 22
- Previous: Bacteria growth model exercises
- Next: Penicillin clearance model exercises
Similar pages
- The idea of a dynamical system
- An introduction to discrete dynamical systems
- Developing an initial model to describe bacteria growth
- Bacteria growth model exercises
- Bacteria growth model exercise answers
- Exponential growth and decay modeled by discrete dynamical systems
- Discrete exponential growth and decay exercises
- Discrete exponential growth and decay exercise answers
- Doubling time and half-life of exponential growth and decay
- Penicillin clearance model exercises
- More similar pages